こんにちは。
GMOアドマーケティングのT.Mです。
前回に引き続き、第2回目の勉強会を実施しました。
今回勉強したことをご紹介します。
期待値
期待値とは、確率変数の値と確率を掛けた合計で、試行した値の平均です。
サイコロの出目によって以下の表の通り賞金がもらえるゲームの場合、
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 賞金 | 10円 | 50円 | 100円 | 100円 | 200円 | 500円 |
| 確率 | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) |
$$10 \times \frac{1}{6} + 50 \times \frac{1}{6} + 100 \times \frac{1}{6} + 100 \times \frac{1}{6} + 200 \times \frac{1}{6} + 500 \times \frac{1}{6} = 160円$$
このゲームの期待値は160円なので、参加費が200円だと参加者は40円損する事になります。
正規分布
得られたデータの母集団分布は、正規分布とみなして良いことが多いです。
正規分布の確率密度関数は、平均をμ、分散を\(σ^2\)とすると下記の通りです。
$$f(x)=\frac{1}{\sqrt{2\pi}σ}exp\{-\frac{1}{2σ^2}(x-μ)^2\}$$
\(N(μ,σ^2)\)と書きます。
特にμ=0, σ=1のものを\(N(0,1^2)\)を標準正規分布といいます。
また確率変数xが\(N(μ,σ^2)\)に従う時、
\(u=\frac{x-μ}{σ}\)は、\(N(0,1^2)\)に従います。
これは、どんな正規分布でも標準正規分布に直せることを表しています。
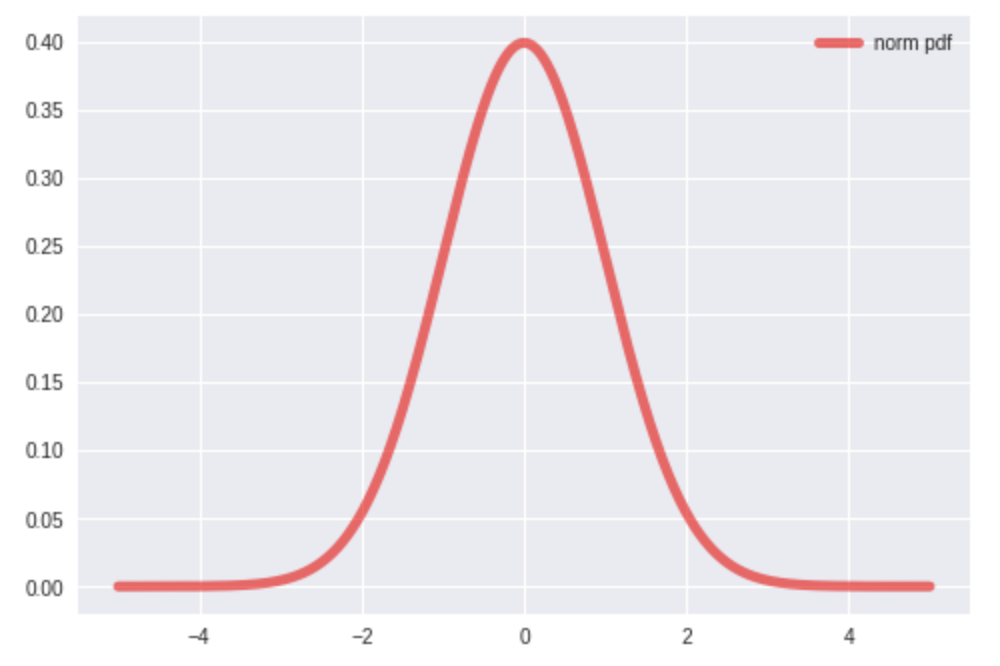
標準正規分布をPythonで書いてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm fig, ax = plt.subplots(1, 1) # -5.0から5.0の数値を10000等分した値 x = np.linspace(-5.0, 5.0, 10000) # 標準正規分布で計算する f = norm.pdf(x, loc=0, scale=1) # グラフにプロットする ax.plot(x, f, 'r-', lw=5, alpha=0.6, label='norm pdf') ax.legend(loc='best', frameon=False) plt.show() |
まとめ
今回は主に正規分布を中心に勉強してきました。
SciPyを使うことで簡単に標準正規分布のグラフが描けました。
これらをどう仕事に活かしていくか、まだまだ勉強は続きます。
以上です。


