GMOアドマーケティングのT.Oです。
はじめに
弊社では自社のアドテクプロダクトをより良いものにするために、広告配信の精度向上や膨大なデータの解析、データからの予測の手段として、機械学習や統計学の技術を数多く取り入れており、すでに本ブログでも機械学習関連の記事をいくつか公開しておりますが、
- 機械学習や統計学を業務に活用できるエンジニアを増やすこと
- データに強いエンジニアを増やすことで、さらにプロダクトを強化すること
- 現場のエンジニアから「機械学習やデータ解析の知識を身につけたい」という声が多くあったこと
という理由から、社内で機械学習、統計学の勉強会を開催しております。
今期は統計学領域の勉強会を開催したので、本記事ではその勉強会で学んだことを紹介します。
今回は第1回です。
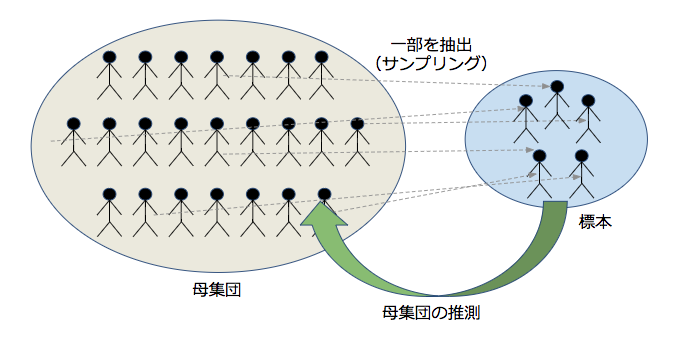
※上記画像は執筆者が作成
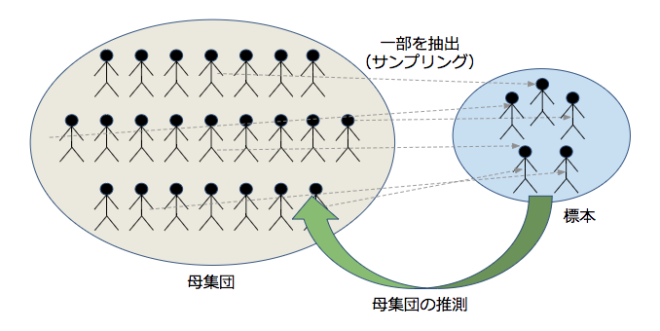
1 母集団と標本
統計解析の対象となる集団全体のことを母集団といいます。
標本とは母集団から一部をサンプリングした部分集合のことをいいます。
2 母数と統計量
母集団にはばらつきがあります。ばらつきの様子は母集団分布とよばれます。
母集団の中心位置をあらわすには母平均、中心位置からの広がり具合をあらわすには母分散や母標準偏差を利用します。
これらの母集団分布の特徴を表すパラメータのことを母数といいます。
実際には母数の値は未知なので、標本データからその値を推測することが統計解析の目的になります。
母数を推測するために計算される量のことを統計量とよび以下のようなものがあります。
(1)平均
$$\overline{x}=\frac{x_1+x_2+…+x_n}{n}=\frac{\sum^n_{i=1}x_i}{n}$$
(2)平方和
$$S=\sum^n_{i=1}(x_i-\overline{x})^2={\sum{x_i^2}}-\frac{(\sum{x_i})^2}{n}$$
(3)分散
$$V=\frac{S}{n-1}$$
(4)標準偏差
$$s=\sqrt[]{V}$$
3 ヒストグラム
母集団分布の様子を調べるのによく用いられるのが度数分布表やヒストグラムです。
ヒストグラムを参照することで中心の位置、ばらつき具合、分布の形(中心に対して左右対称になっているか)などをより詳しく調査することができます。
(1)度数分布表の例(身長)
| 区間 | 中心値 | 度数f | X | fX | fX^2 |
| 155〜160 | 157.5 | 4 | -3 | -12 | 36 |
| 160〜165 | 162.5 | 10 | -2 | -20 | 40 |
| 165〜170 | 167.5 | 28 | -1 | -28 | 28 |
| 170〜175 | 172.5 | 35 | 0 | 0 | 0 |
| 175〜180 | 177.5 | 17 | 1 | 17 | 17 |
| 180〜185 | 182.5 | 4 | 2 | 8 | 16 |
| 185〜190 | 187.5 | 1 | 3 | 3 | 9 |
| 190〜195 | 192.5 | 1 | 4 | 4 | 16 |
| 合計 | 100 | -28 | 162 |
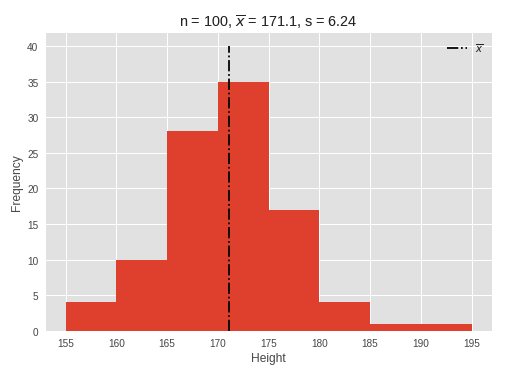
(2)ヒストグラムの例
度数分布表の例の元データを利用し、Pythonのグラフライブラリ(matplotlib)を使用してヒストグラムを作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
import matplotlib.pyplot as plt import numpy as np import math data = [185.7, 181.8, 175.4, 168.7, 176.1, 173.6, 171.2, 169.6, 174.7, 173.2, 164.5, 166.8, 159.7, 168.0, 171.1, 162.5, 172.1, 168.8, 169.4, 170.9, 172.1, 167.1, 173.3, 169.2, 176.9, 158.8, 171.8, 178.9, 169.0, 173.7, 181.4, 190.4, 175.7, 169.8, 175.3, 175.7, 168.9, 164.1, 176.4, 180.2, 174.5, 164.1, 170.0, 168.7, 171.0, 181.9, 169.6, 168.5, 174.7, 158.7, 168.6, 177.4, 171.3, 173.0, 165.3, 172.0, 166.3, 169.7, 175.0, 176.0, 169.9, 172.2, 169.3, 172.4, 166.0, 161.9, 177.7, 170.2, 177.1, 163.8, 171.5, 177.7, 170.6, 165.9, 175.6, 173.9, 170.4, 164.0, 165.5, 174.7, 174.9, 170.3, 169.4, 160.4, 158.3, 171.6, 173.5, 172.7, 161.6, 168.2, 171.8, 178.9, 160.0, 173.3, 167.5, 165.3, 168.8, 173.5, 178.2, 170.8] fig, ax = plt.subplots() # data:グラフデータ, bins:棒グラフの本数(区間数), range:グラフデータの範囲を設定する n, bins, patches = ax.hist(data, bins=8, range=(155, 195)) # 平均の計算(度数の一番大きい区間の値(中心値)と他の区間との差異から計算します) x_bar = 172.5 + 5.0 * (-28) / 100 # 分散の計算 V = 5.0 ** 2 * (162 - (-28) ** 2 / 100) / 99 # 標準偏差の計算 s = round(math.sqrt(V), 2) # グラフのタイトルを設定する title_str = 'n = ' + str(len(data)) + ", $\overline{x}$ = " + str(x_bar) + ', s = ' + str(s) ax.set_title(title_str) # x軸のタイトル ax.set_xlabel('Height') # x軸のラベル xlabel = [ '155', '160', '165', '170', '175', '180', '185', '190', '195' ] # ラベルを設定するx軸の位置(度数表の区間に設定した値) ax.set_xticks([155.0, 160.0, 165.0, 170.0, 175.0, 180.0, 185.0, 190.0, 195.0]) # x軸にラベルを設定する ax.set_xticklabels(xlabel) # y軸のタイトル ax.set_ylabel('Frequency') # 平均の線を引く plt.vlines(x_bar, 0, 40, linestyle='dashdot', label="$\overline{x}$") plt.legend() # 描画 plt.show() |
4 感想
今回は母集団と標本の概念、母集団の分布の様子を調べるのに用いられる度数表やヒストグラムについて紹介しました。
度数表やヒストグラムを作成することで、生のデータを眺めるだけではわかりにくいデータの特徴を把握しやすくなりますので積極的に活用しようと考えています。