こんにちは。
GMOアドマーケティングのK.Mです。
今回の勉強会では分散分析の二元配置法について学びました。
アイディア 💡 は組み合わせと言いますが、AとB(2つ要因)の組み合わせを分析したいケースは多く、そんな時に役立つ分析手法です。
・繰り返しのない二元配置
・繰り返しのある二元配置
を学習しましたが、下記2つの利点から「繰り返しのある二元配置」の手法を紹介します。
- 2回以上のデータ(繰り返し)があれば、A、B、2つの要因の間の交互作用を解析できる
- 繰り返す事で、サンプリング誤差が原因で正しく検定できない割合も減らせる(検出力が上がる)
繰り返しのある二元配置を試してみよう
Pythonも関数がありますが、誰でもお手軽に試せる(分散分析表が作成できる)、
こちらのエクセルを利用する方が簡単でしたので紹介します。
■事前準備
エクセル2016の分析ツールのアドオンを利用できる状態にします。
■課題
牛の成長に繋がる5種類の草と、4種類の餌との二元配置の分散分析
手順1.組み合わせによる成長(繰り返しあり)データをエクセルシートに記載
| 草 | トウモロコシ | 大豆 | 綿実 | 麦 | 水 |
|---|---|---|---|---|---|
| 1 | 5 | 4 | 0 | -8 | 4 |
| 17 | 6 | -2 | 0 | 0 | |
| 2 | 20 | 10 | 11 | 4 | 16 |
| 38 | 24 | 17 | 0 | 24 | |
| 3 | 10 | 13 | 22 | 15 | 19 |
| 6 | 15 | 18 | 25 | 33 |
手順2.データ>データ分析>【分散分析:繰り返しのある二元配置】を選択
手順3.必要なデータを入力します。入力範囲は表の項目名まで選択します。
1標本あたりの行数とは組み合わせの反復数なので、2を入力。結果は、新規ワークシートが楽です。
手順4.新規ワークシートに各要因の平均値が以下のように生成されます。
- 標本(草)はP-値がきわめて小さいので、きわめて高度に有意差が検出できました。
- 列では10%の有意水準で有意でした。交互作用も5%水準で有意でした。
| 分散分析表 | 平方和S | 自由度Φ | 平均平方V | 分散比F0 V?/VE |
有意確率P
Pr(F≧F0(?))
|
棄却域境界値 F(Φ?,ΦE;0.01) |
|---|---|---|---|---|---|---|
| 変動要因 | 変動 | 自由度 | 分散 | 観測された分散比 | P-値 | F 境界値 |
| 標本(草:A) | 1389.6 | 2 | 694.8 | 17.37 | 0.000125 | 3.68232 |
| 列(餌:B) | 412.8 | 4 | 103.2 | 2.58 | 0.079965 | 3.055568 |
| 交互作用A☓B | 998.4 | 8 | 124.8 | 3.12 | 0.027486 | 2.640797 |
| 繰り返し誤差 E | 600 | 15 | 40 | |||
| 合計 | 3400.8 | 29 |
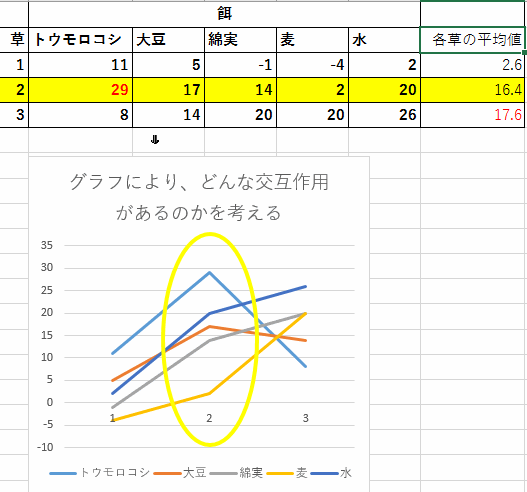
手順5.各組み合わせの平均値を計算されるので、これを利用してグラフ化します。
- 交互作用がなければ、3番目の草が良いという結論ですが、とうもろしと相性が悪い。
- 交互作用がある為、草と餌の両方を見て2番めの草と、とうもろこしの組み合わせが良いと結論付けます。
まとめ
交互作用とは2つの因子が組み合わさることで初めて現れる相乗効果。
結婚している人たちが離婚する割合は、3組に1組ではなく、
約0.5パーセントって知ってました? 相乗効果を発見するって何だかロマンチックですね 😛
ネットで多く目にするのは読み合わせでしょうか。次々と関連記事を読み続ける人が多ければ、
あわせて読みたい記事をオススメできている事になると思います。
弊社では、TAXELというサービスがありますが、ユーザーの方が求めている記事や広告を
お届けできるよう統計を理解してシステムを改善し続けたいと思います。



