このエントリーは、GMOアドマーケティング Advent Calendar 2018 の 12/16 の記事です。
GMOアドマーケティングとしては初のAdvent Calendar参戦です。
はじめに
こんにちは。GMOアドマーケティングのS.S.です。
通販サイトや動画配信サイトにおけるアイテム推薦では、ユーザーが購入・視聴などを行なったアイテムにつけたスコアをもとにして、そのユーザーが興味を持つであろうアイテムを提示することがあります。
そうした設定では行と列をそれぞれアイテムとユーザーに対応させて、セルの値として列に対応するユーザーが行に対応するアイテムに対してつけたスコアを持つ行列を考えることができます。
行列分解ではユーザーとアイテムにそれぞれ低次元のベクトルを割り当て、それらの積としてスコアを説明します。
今回の記事では行列分解の単純なケースについて座標降下法を使ってパラメータを求める更新式を見ていきたいと思います。
座標降下法による行列分解
座標降下法では目的関数を一つの変数ずつ最小化していきます。
勾配降下法などと比べて座標降下法を使う利点の一つとして学習率のようなパラメータを調整する必要がないということがあります。
![]()
目的関数がある程度よい関数の場合は、各変数についての微分を0とおいた式を解いて座標ごとの更新式を導出し、各座標について更新していくことを繰り返すことでfを最小化できます。
この後の説明で使う記号をいくつか決めておきます。
I, Jをそれぞれアイテム数, ユーザー数とします。
さらにXを入力のスコア行列(I × J)、Uをアイテムに対応するベクトルからなる行列(I × K)、Vをユーザーに対応するベクトルから行列(J × K)ととします。
行ベクトルはui, vjなどと書くことにします。
今回の設定ではXをUVTとして近似するイメージになります。
最小化するのは次の目的関数です。
アイテムとユーザーのベクトルの内積と、ユーザーのつけたスコアの差の2乗和に正則化項を加えたものとなっています。
Uの一つの変数について微分を0として式を解くと3行目の更新式が得られます。
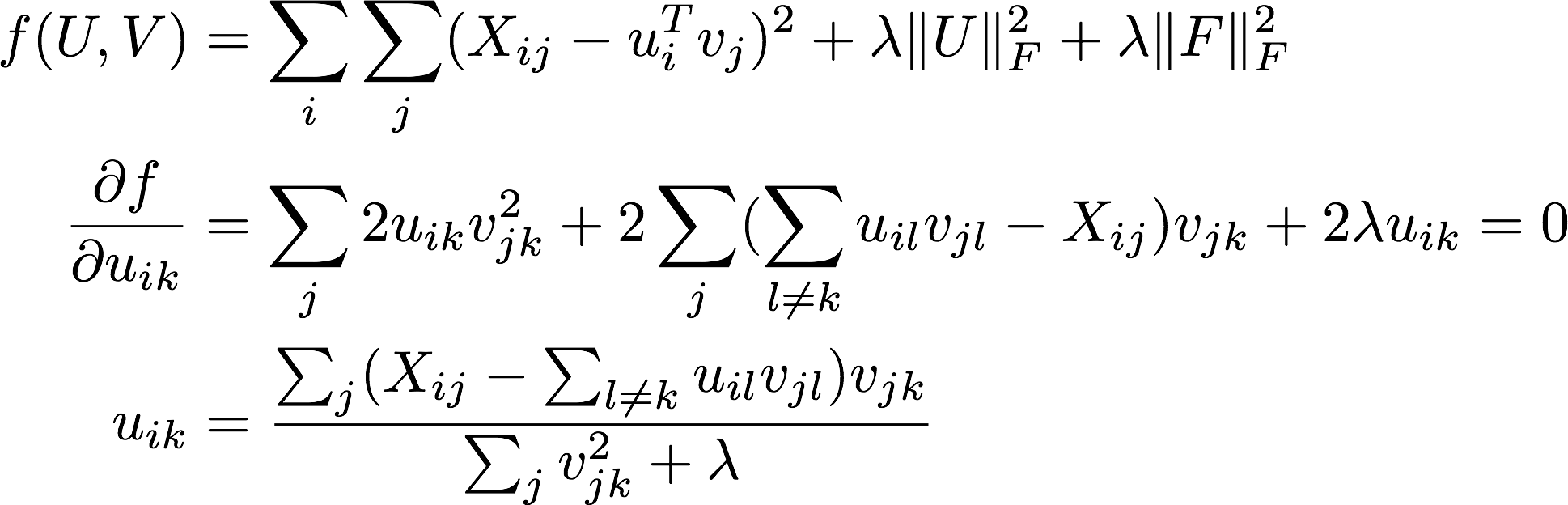
VについてもUとVを入れ替えて同様に更新式が得られます。
全ての変数について一通り更新したら最初に戻って更新を繰り返します。
行列にスコアが入っていないセルがある場合は上の損失関数のセルごとの和をとっているところで、マスク行列をかけて上記と同様の流れで更新式を導出できます。
最後に
この記事では行列分解のシンプルなケースについて座標降下法による更新式を確認しました。
冒頭ではアイテム/ユーザー行列にスコアが入っているという設定を例としましたが、他の例として単語の共起行列やドキュメントと単語のカウント行列に適用して単語や文書のベクトルを得ることもできます。
明日は、非エンジニアでも使い回せる、UiPathでつくる簡易botについてのお話です。
お楽しみに。
クリスマスまで続くGMOアドマーケティング Advent Calendar 2018
ぜひ今後も投稿をウォッチしてください!
■エンジニアによるTechblog公開中!
https://techblog.gmo-ap.jp/
■Wantedlyページ ~ブログや求人を公開中!~
https://www.wantedly.com/projects/199431
■エンジニア採用ページ ~福利厚生や各種制度のご案内はこちら~
https://www.gmo-ap.jp/engineer/
■エンジニア学生インターン募集中! ~有償型インターンで開発現場を体験しよう~
https://hrmos.co/pages/gmo-ap/jobs/0000027



