こんにちは、GMOアドマーケティングのMHです。
現在、GMOアドマーケティングでは機械学習の勉強会を行っています。
ゼロから作るDeep Learningをみんなで輪読をしているのですが、出来るだけ数式を使わないでコードで説明しようとしてくれているため、非常に分かりやすいです。
ただ、それでも章を進むに連れて、前提となってくる用語などが増えてきますので、「あれこの用語なんだっけ?」となることがしばしばありました。
これからゼロから作るDeep Learningを読む人が同じようなことにならないように本書に出てくる必須と思われる用語についてまとめてみました。
活性化関数
総入力を入力として、出力が切り替わる関数のことを指します
パーセプトロンではステップ関数が使われ、ニューラルネットワークではシグモイド関数/ReLU(ランプ関数)がよく使われます。
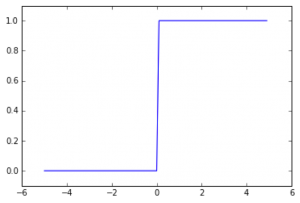
ステップ関数
閾値を境に出力が切り替わる関数のことです。
そのため、ステップ関数は一定値を超えると急に値が切り替わる様な動きをします。
例えば、xが0以下だと0となり、0より大きいと1となるような関数です。
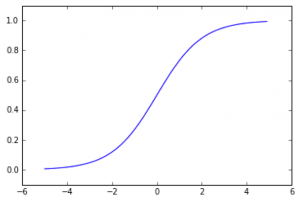
シグモイド関数
以下の数式で表される関数のことです。
1/(1+exp(-x))
シグモイド関数はステップ関数とは違い、数字が入力値によって連続して変化していき、緩やかな逆S字の出力となります。
ニューラルネットワークやディープラーニングでは以下の理由により、よく使われます。
- 必ず傾きが求まる(必ず微分可能)
- 出力が0−1に収まる
- 誤差逆伝播法で微分する際の計算コストが軽い
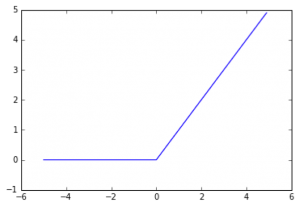
ReLU関数(ランプ関数)
入力が0以下なら0、0以上ならそのまま出力する関数のことです。
以下の数式で表せます。
h(x) = {x(x>0),0(x<=0)}
誤差逆伝播法を使用した際の逆伝播時の動作としては、以下のようになります。
- 0以下なら伝播をストップ(0を流す)
- 0以上ならそのまま流す
ニューラルネットワークにおける活性化関数
ニューラルネットワークは簡単に表すと以下の構成になっています。

入力層から隠れ層などの次の層に遷移得する際に活性化関数を通して値を変化させていきます。
ニューラルネットワークでの活性化関数には線形関数は使わず、非線形関数である必要があります。
線形関数では、入力が単に等倍されるだけとなってしまい、ニューラルネットワークの隠れ層を増やす意味が無いからです。
出力層は最終的に出てきた値を求める値かどうかを判定や分類するための層となります。
そのため、出力層に遷移する際にはそれまでとは別の活性化関数を利用します。
出力層で利用される活性化関数
恒等関数
出力をそのまま利用します。
回帰問題で利用されます。
ソフトマックス関数
出力結果の総和を自分自身の値で割ります。つまり、出力結果に対する割合を表します。
分類問題で利用されます。
損失関数
活性化関数を利用して、出た結果を元に重みを増減するときに利用する関数です。
重みの増減は微分を用いてどの程度移動するかを算出します。
なぜ、活性化関数そのままではなく、損失関数を通して調整をするのかというと、活性化関数の値そのままでは、振れ幅が大きすぎてしまい、パラメータの調整が難しいためです。
損失関数を通すことによって、パラメータの微妙な動きに出力を連動させ、出力の値を連続的な数値に均す事ができます。
損失関数の種類
2乗和誤差
全部の正解データと出力データとの差を2乗します。
そのため、必ず正の値になります。
Pythonでの実装例としては以下となります。
|
1 2 |
def mean_squared_error(y, t): return 0.5 * np.sum((y-t)**2) |
交差エントロピー誤差
正解ラベルに対する出力の自然対数とします。
Pythonでの実装例としては以下となります。
|
1 2 3 |
def cross_entropy_error(y, t): delta = 1e-7 return -np.sum(t*np.log(y+delta)) |
ソースコード上にてdeltaを足しているのはyが0の場合、log(0)=マイナスの無限大での計算が発生してしまい、計算を進めることが出来なくなってしまうためです。
勾配法(勾配降下法)
勾配法には以下の2種類があります。
- 最小値を求めるのが勾配降下法
- 最大値を求めるのが勾配上昇法
機械学習では基本的には、損失関数を最小化するように重みを更新するため勾配降下法が利用されます。
重みの更新は、入力〜出力→損失関数の一連の数式に対して、微分を行い、重み移動を少しずつ繰り返すことで、損失関数を最小化させていきます。
ミニバッチ
訓練データの中からランダムにデータを抜き出して学習をさせることをミニバッチといいます。
ミニバッチを利用するということは、一部のデータを全体の近似として利用することになります。
ミニバッチにおける損失関数の計算について
損失関数の計算は抜き出した訓練データ1つ1つに対して求める必要はなく、
最終的な損失の値を訓練データの数で割ることで平均の損失値を求める形になります。
なぜなら、最終的な目的は、全ての訓練データで、損失の値を0にすることのため、全体として損失最小化をすれば良いため、平均を求める形となります。
誤差逆伝播法
勾配法によって重みを更新するには勾配を求める必要がありますが、数値微分で求めてしまうと非常に多くの時間がかかってしまいます。
そのため、解析的に数式を説いて求める方法として、誤差逆伝播法を利用します。
数値微分が全く使われないかというとそうではなく、数値微分の利点としては実装の簡単さがあげられます。
そのため、誤差逆伝播法の結果確認として数値微分を利用する事に利用されます。
如何でしたでしょうか。
今回はゼロから作るDeep Learningに出てくる基本的な用語について纏めました。
機械学習に興味がある方は、本記事を片手に是非、ゼロから作るDeep Learningを読んでみてください。