GMOアドマーケティングのy.yです。
社内の統計勉強会も大分終盤に差し掛かってきました。
第8回目では前回の分散分析の続きと相関分析について学びました。
※前回のブログは下記です。
今回は相関係数と散布図について簡単にまとめたいと思います。
まずは相関係数と散布図について
- 相関係数
- 2つの確率変数の間にある線形な関係の強弱を測る指標である。相関係数は無次元量で、ー1以上1以下の実数に値をとる。相関係数が正のとき確率変数には正の相関が、負のとき確率変数には負の相関があるという。また相関係数が0のとき確率変数は無相関であるという。引用元 | 相関係数、2018年5月30日、https://ja.wikipedia.org/wiki/相関係数
- 散布図
- 散布図は、縦軸、横軸に2項目の量や大きさ等を対応させ、データを点でプロットしたものである。各データは2項目の量や大きさ等を持ったものである。日本工業規格では、「二つの特性を横軸と縦軸とし、観測値を打点して作るグラフ表示」と定義している。散布図には、2項目の分布、相関関係を把握できる特徴がある。データ群が右上がりに分布する傾向であれば正の相関があり、右下がりに分布する傾向であれば負の相関がある。相関係数が0であれば無相関となる。引用元 | 散布図、2018年5月30日、https://ja.wikipedia.org/wiki/散布図
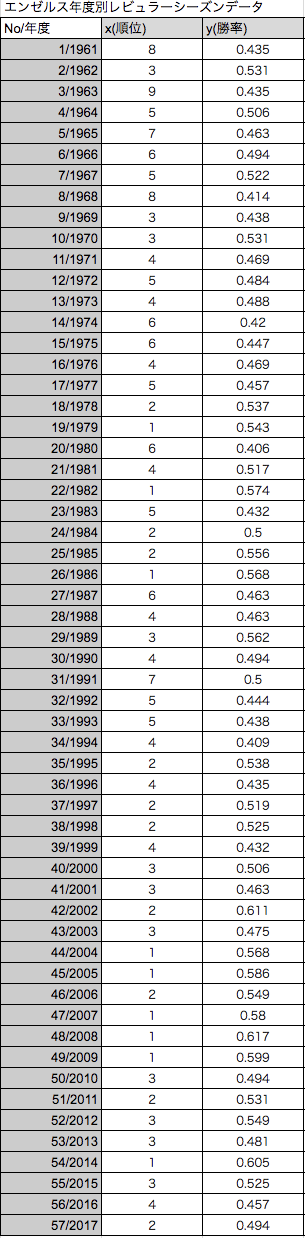
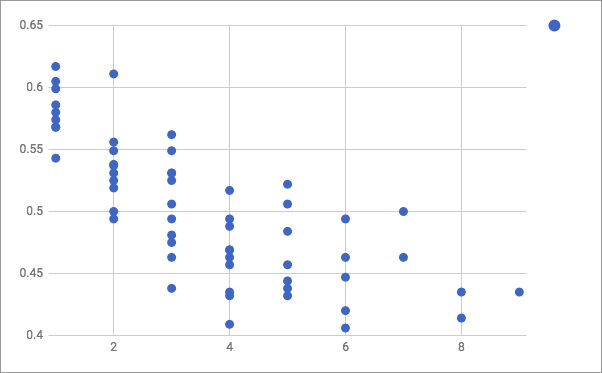
例)二刀流でメジャーリーグでも話題の大谷翔平選手が所属するロサンゼルス・エンゼルスがレギュラーシーズンで何位くらいになるのか過去のデータからGoogle スプレッドシートでを使って散布図を作って見ます。
相関係数=共分散÷(xの標準偏差×yの標準偏差)
相関係数= -4.773473684 / √225.5087719 * 0.1761935789 = -0.7572822441
-0.7572822441なので負の相関があります。
Google スプレッドシートでの散布図作成方法
- ツールバーの”・・・”を選択し、グラフを挿入をクリックします。
- グラフの種類:散布図
- データ範囲:上記のエンゼルス年度別レギュラーシーズンデータの順位と勝率を指定
※2018/05/24時点のエンゼルスの順位と勝率
アメリカンリーグ西地区で3位の勝率0.542
レギュラーシーズンを1位で終わるには0.6くらいになっておきたい感じです。
2002年は勝率が0.611だったが2位だったのでかなり接戦だったのでしょう。
引用:Wikipedia 2002年のメジャーリーグベースボール
まとめ
統計のブログというよりメジャーリーグの色が強いブログになってしまいましたが順位と勝率の相関関係が把握できました。
業務ではWeb広告の不正について相関係数と散布図から
不正原因を可視化し、アドフラウド関連に活用できるのではないかなと思いました。
※11月現在
結果的にエンゼルスは80勝、82敗 勝率0.494の4位でシーズンを終了しました。


