半環と図 | GMOアドパートナーズ TECH BLOG byGMO

こんにちは。GMO NIKKOのshunkiです。

最近、ChatGPTなどの大規模言語モデルの出現によって、平易な説明が不要になってきた気がします。なぜなら目の前の文章が難解だと感じても、大規模言語モデルが文意を紐解いてくれるからです。そうなると、興味深い情報が詰め込まれた文章でさえあれば、読み手にとっては十分ではないでしょうか。

さて、簡単な予防線も張ったところで、ここから先は大した説明もなく専門用語を使っていく。用語に興味がそそられれば、その用語を中心に周辺知識を調査すると楽しいだろう。あるいは話の流れ上、図が多くなるので、図を眺めるだけで何らかの直感が働くこともあるだろう。

この記事では、半環とよばれる代数的構造と図の相性の良さについて垣間見ることを目標とする。

記事の流れとしては、最初に図をさまざまに解釈しながら眺めていく。次に半環の定義と、半環と整合する図を導入する。そして、半環と整合する図が図のまま解釈（計算）できること、関数として解釈できること、行列として解釈できることを見る。

この記事から得られる可能性は、あなたが何気なく描いた図から、多様な解釈を引き出せる可能性である。あるいは、概算値でも図に半環の値を載せてみれば、想像だにしなかった解釈（計算結果）という気づきを得られる可能性である。また、図を関数や行列として捉え直す視点が得られる可能性である。

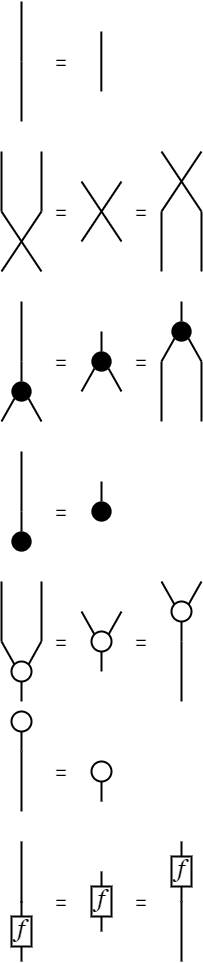
図の解釈を取り替える

さっそくだが、次の図の四角い箱の中身に値をはめ込むことで、いくつかの異なる解釈を与えていく。

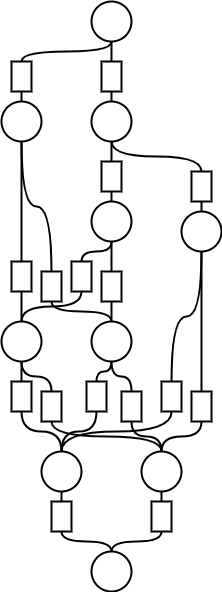
パターンの数え上げ

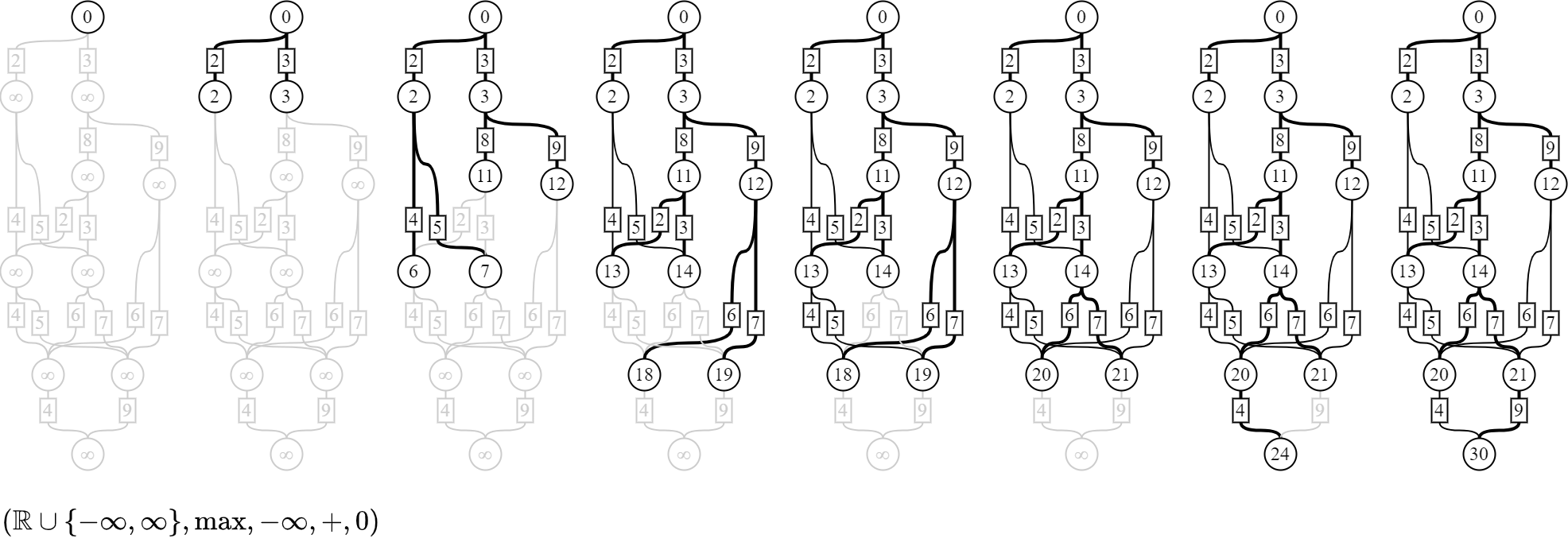
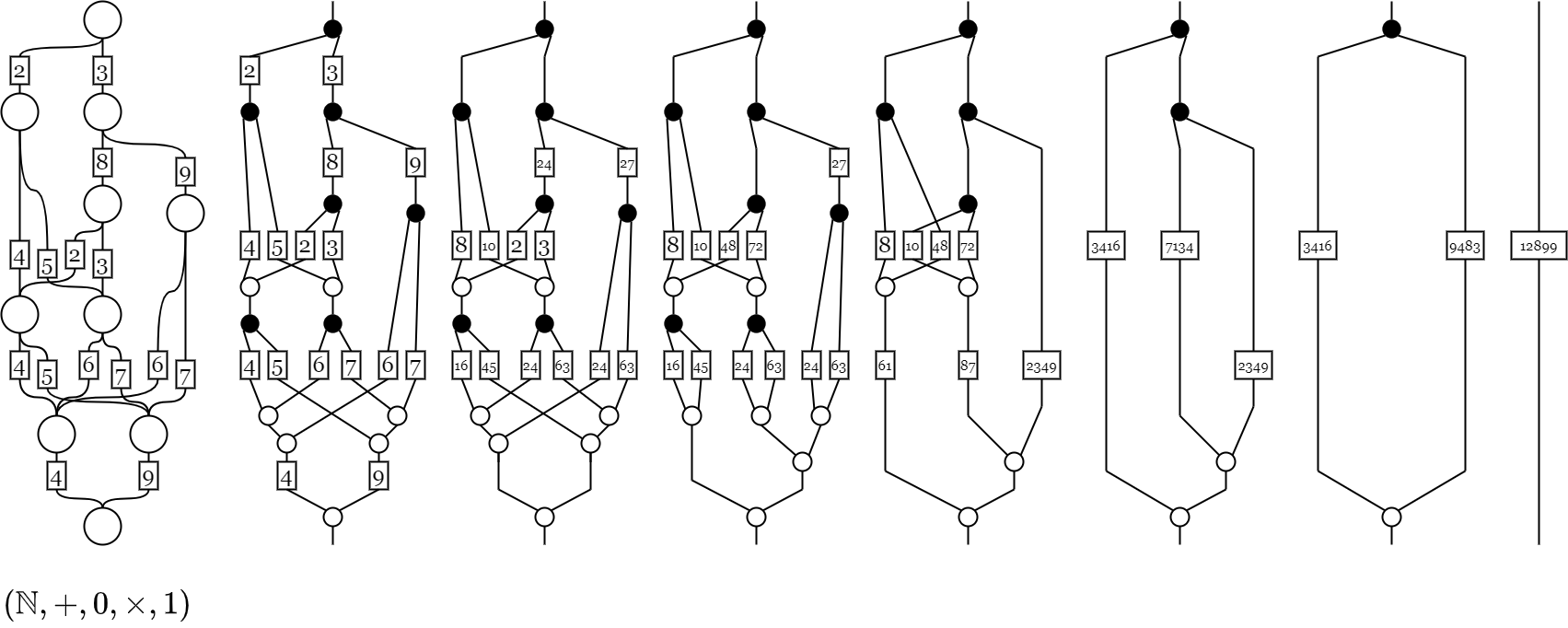
ぱっと見、複雑そうな図だが、実際にその複雑さを計算してみよう。例えば、図の四角に適当な自然数をはめ込んでみる。

上にある丸から、下にある丸へ移動するときのパターン数を四角の値が表すとしよう。すると、この図はパターンの数え上げとして解釈できる。上から順にパターン数を数え上げていくと、次の図のように計算される。

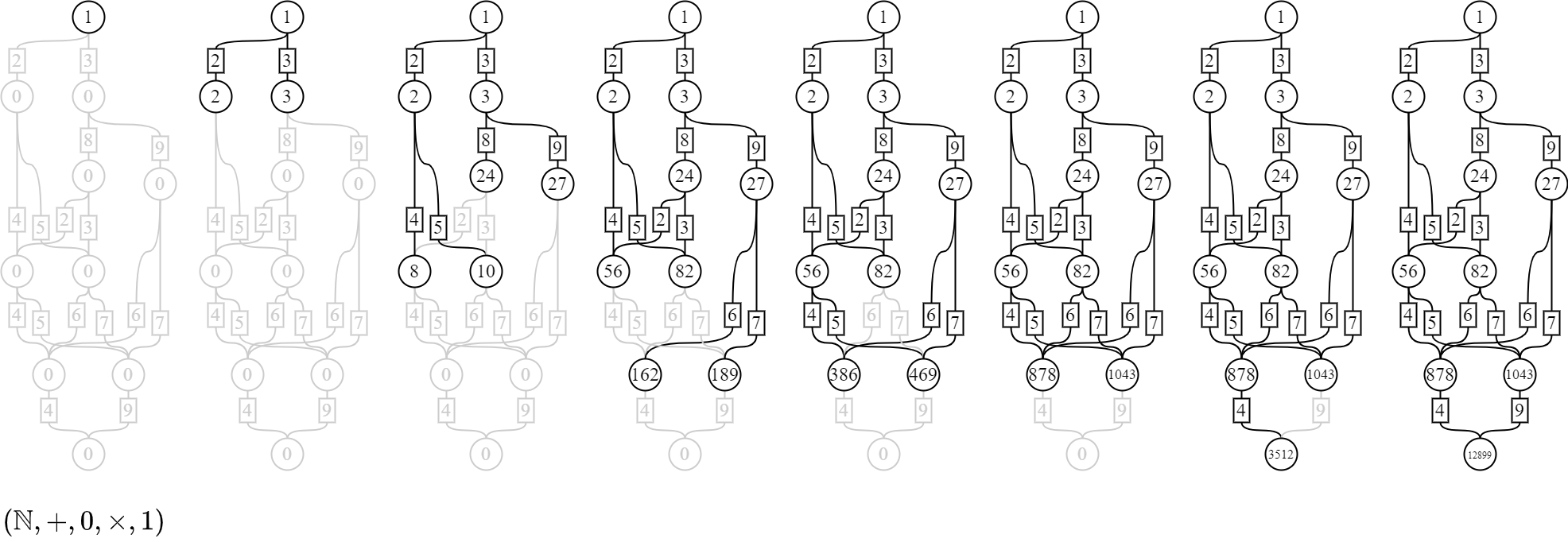
四角には1桁の値しかはめ込んでいないのに、上の図の結果は約1万という巨大なパターンが生まれている。値の大きさに肯定的な意味づけをするなら、それぞれは一桁に収まるような簡単な仕組みであっても、それらを組合せ可能にするだけで、驚くほど豊かな表現力を提供できることが示唆されている。反対に値の大きさに否定的な意味づけをするなら、それぞれが把握可能な複雑さであったとしても、全体では制御不能な複雑さに膨らむ可能性が示唆されている。

なお、細かいことを言えば、計算方法にはプッシュ型とプル型がある。上の図はプッシュ型で計算している。プッシュ型は、パターンを数え終わった丸があれば、下の丸に足し込んでいく（プッシュする）。例えば、値の確定した(24)の下に[2]-(8)が伸びていれば、8に48（=24×2）を足し込んで、(24)-[2]-(56)へ更新する。上の図では、グレーアウトされていた結線が黒になったさいにプッシュしている。

プル型は、上にある丸がすべて数え終わっていれば、一気に計算する（プルする）。例えば、数え終わってない丸( )の上に、数え終わった丸である(2)-[4]-と(24)-[2]-があれば、(56)へ更新して数え終える（56=2×4+24×2）。

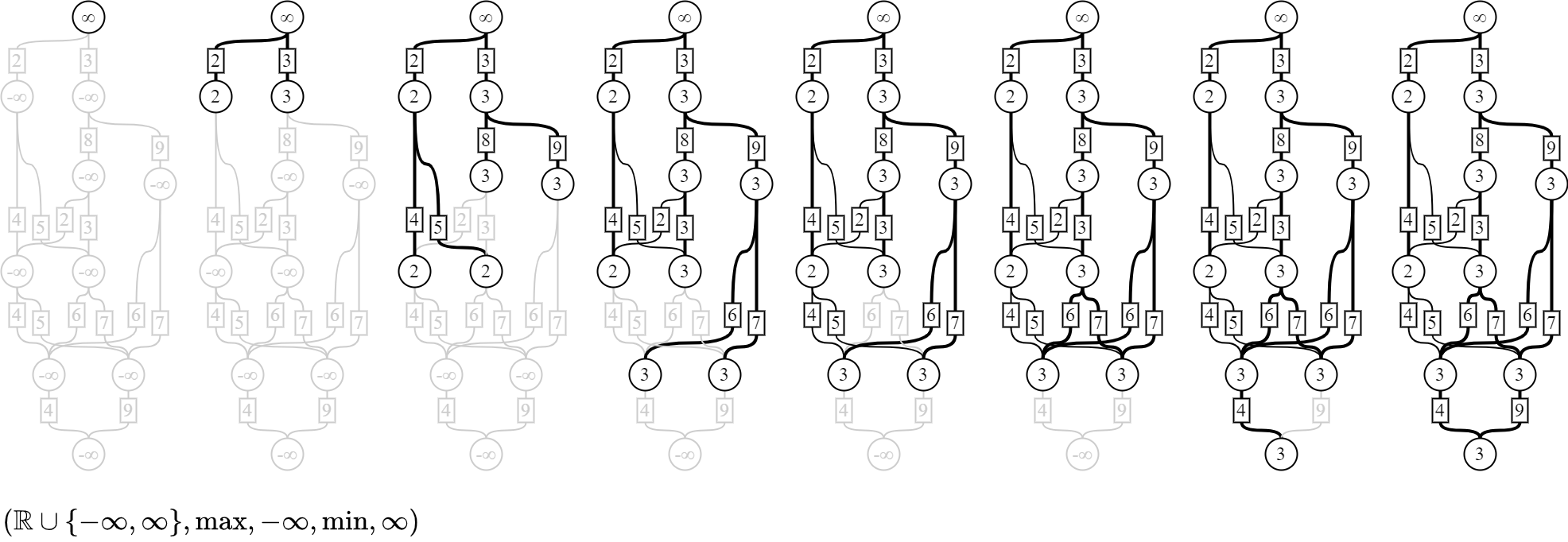
最大パターン

では、もしも１つの経路しか選べないとしたら、どの経路を通ると最もパターン数が大きくなるだろうか。上から順に最大パターン数を選択していくと、次の図のように計算される。これは自然数の足し算の代わりに、２つの自然数から大きい方の自然数を選ぶmax演算を使って計算している。

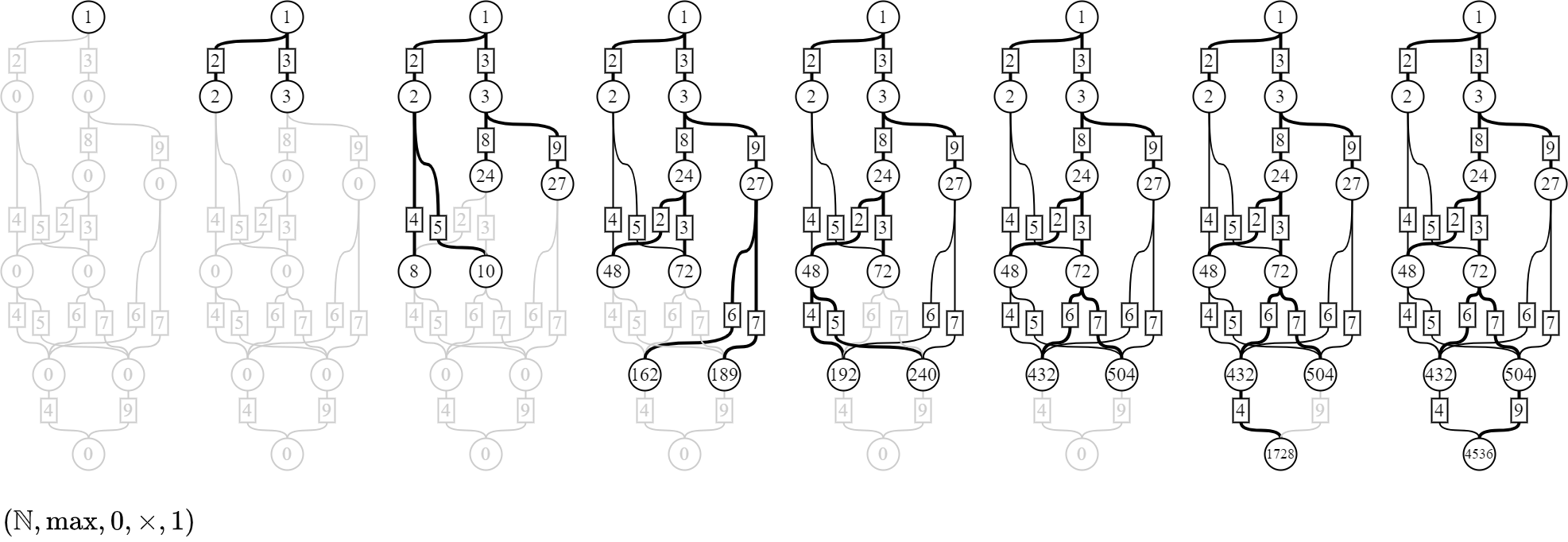
結果は4536（=3×8×2×7×9）パターンとなった。値の大きさに肯定的な意味づけをするなら、積極的に「3×8×2×7×9」の経路を選択するように注力すべきだろう。反対に値の大きさに否定的な意味づけをするなら、「3×8×2×7×9」の経路を選択することは極力避けるべきだろう。なお、この計算方法はビタビアルゴリズムへつながる。

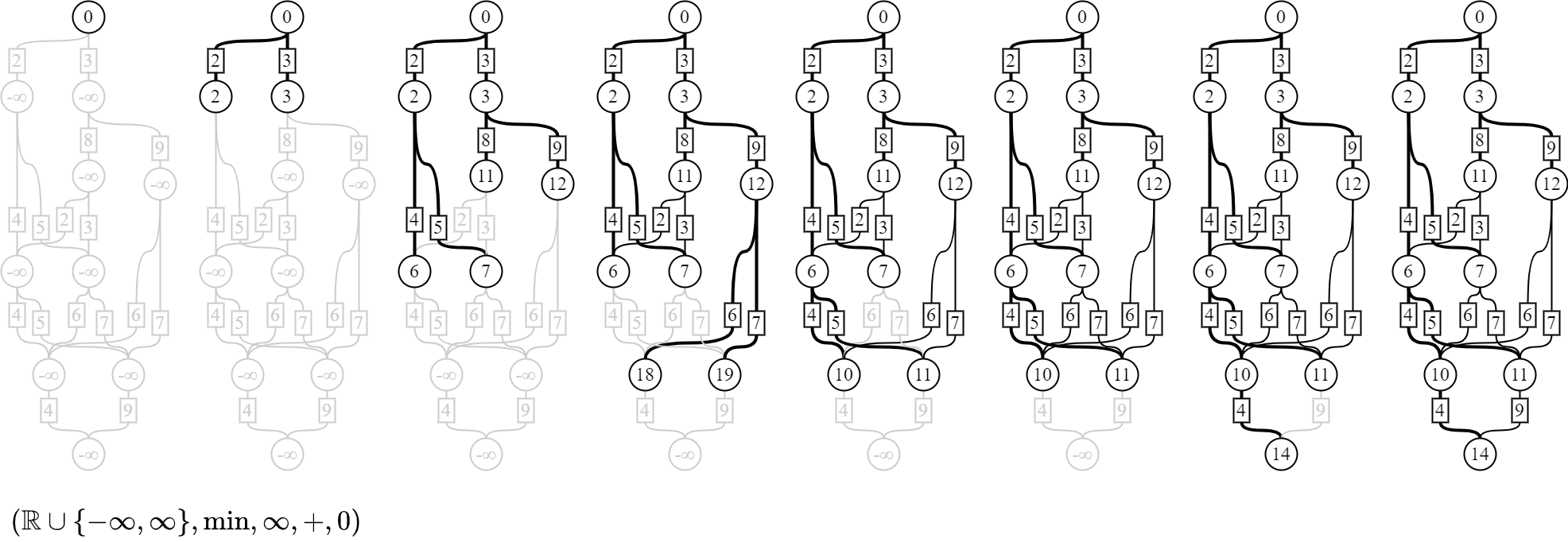
最小パターン

もしも１つの経路しか選べないとしたら、逆に、どの経路を通ると最もパターン数が小さくなるだろうか。上から順に最小パターン数を選択していくと、次の図のように計算される。

これは自然数の足し算の代わりに、２つの自然数から小さい方の自然数を選ぶmin演算を使って計算している。ただし、自然数でない値として「∞」を形式的に導入する。このとき、任意の自然数nについて、「n×∞ = ∞ = ∞×n」とし、「min(n, ∞) = n = min(∞, n)」と定義する。 ∞は計算を整合させるための形式的な値（記号）であって、それ以外の意味は与えられていない点に注意してほしい。小難しく言えば、半群であるminをモノイドとして扱えるように単位元∞を添加し、∞が掛け算のゼロ元として振る舞うよう掛け算を拡張している。

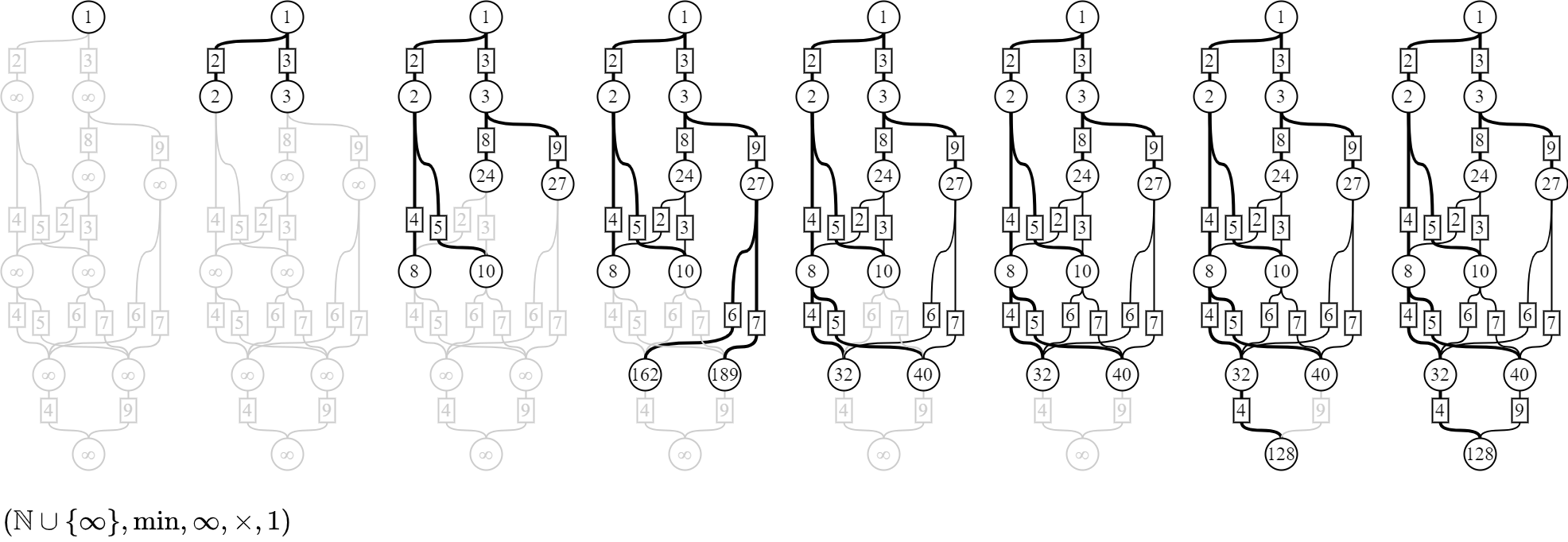
結果は128（=2×4×4×4）パターンとなった。値の小ささに肯定的な意味づけをするなら、積極的に「2×4×4×4」の経路を選択するように注力すべきだろう。反対に値の小ささに否定的な意味づけをするなら、「2×4×4×4」の経路を選択することは極力避けるべきだろう。

最長と最短

maxやminはそのままに、掛け算を足し算へ変えれば、最長や最短の経路が計算できる。

このような計算はトロピカル幾何学と呼ばれ、通常の足し算と掛け算を対数で変換し、極限を取った計算とみなすこともできる（Maslovの脱量子化）。この極限について詳しく知りたい場合、トロピカル幾何学や対数半環（Log semiring）を調べると良い。

なお、最長路の計算はクリティカルパスにつながる。一方の最短路の計算はダイクストラ法に似ている。実際、この記事で見ている計算は、グラフの形状がDAG（有向非巡回グラフ）であるという制限を加えたダイクストラ法とみなせる。もっと味気なく言えば、この記事の図は動的計画法の計算をしているに過ぎない。そして、プッシュ型とはいわゆる配るDPで、プル型とはいわゆる貰うDPである。

最大と最小

minとmaxを組み合わせれば、道に上限のある最大経路、道に下限のある最小経路が計算できる。

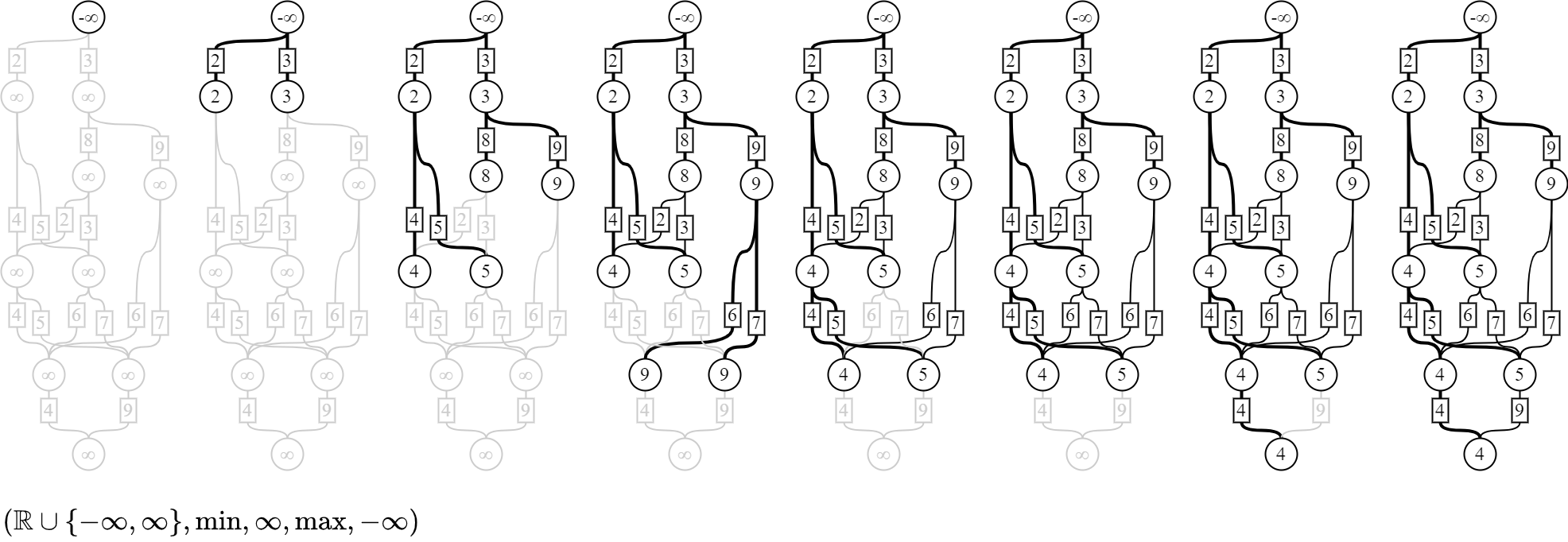
１つ目の計算の意味づけとしては、セキュリティクリアランスレベルなどが考えられる。四角の中の値以上のセキュリティクリアランスレベルがあれば通れるとしよう。すると図のとおり、少なくとも4レベル以上あれば上から下へ到達できる。

２つめの計算であれば、車両の高さ制限などが考えられる。四角の中の値の単位がメートルであるとしよう。すると図のとおり、高さ3メートル以下の車両であれば、上から下へ到達できる。

orとand

値を0と1に限ってmaxとminを考えると、論理演算とみなせる。すなわち、0がFalse（偽）、1がTrue（真）、maxがor（論理和）、minがand（論理積）である。 1は可達性として意味づけできる。つまり次の図のとおり、1のみを通って上から下へ到達できる。

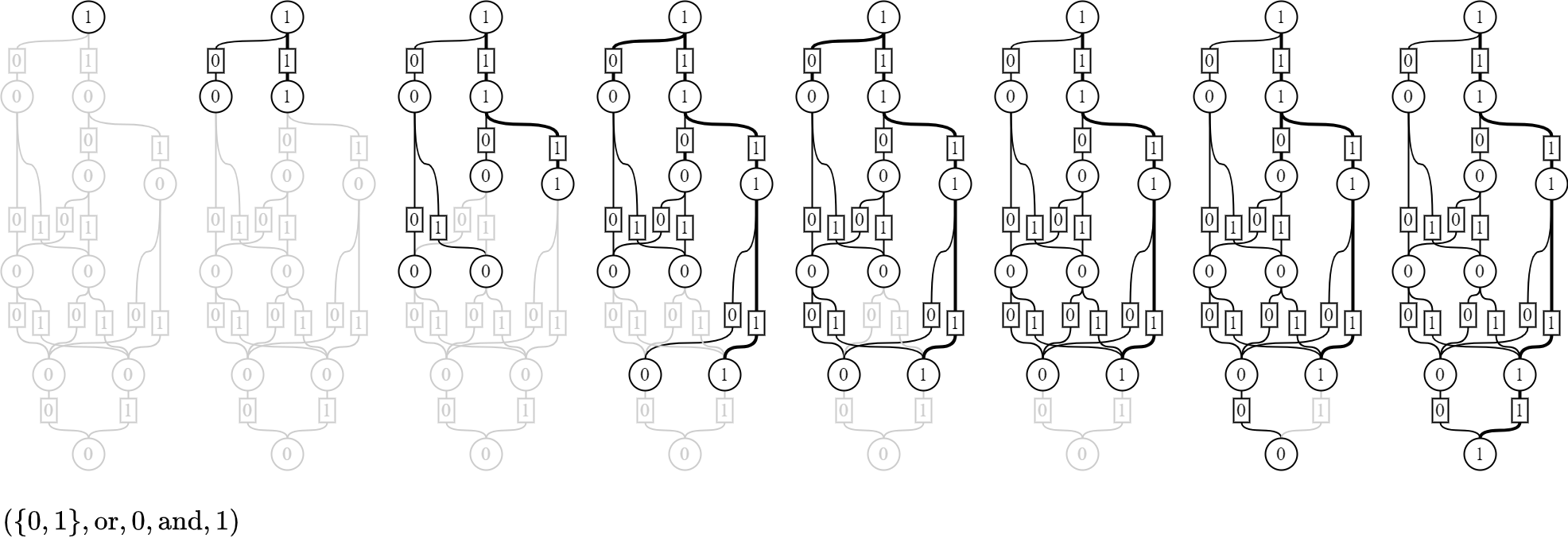
ゼロ環

値を0に限れば、すべての演算が自明に成り立つ（0+0=0と0×0=0）。およそ意味のない計算のように思えるが、図が規則を遵守しているかを確かめるのに役立つことがある。具体的には、後述する項数と余項数に不整合がないかだけを計算したいときに使える。

半環

ここまで見てきたように、図の解釈は様々に取り替えられる。このような多様な解釈をもたらす演算体系（代数的構造）は半環と呼ばれる。半環を意識して図を見ると、四角の中の値は半環の積とみなせ、頂点での合流は半環の和（有限和）とみなせる。なお、分岐は値の複製（有限複製）である。

形式的には、半環(R,＋,O,×,I)の構成要素は次のとおりだ。ただし、以下は参考情報であって、特に覚える必要はない。

Rは台集合（図で言えば、重みとなる値の集まり）
＋: R²→R¹はRの値の2つ組をRの値にうつす写像（２項演算）で、和と呼ばれる。
O: R⁰→R¹は単元集合R⁰（値が1つだけしかない集合）の値をRの値にうつす写像（０項演算）で、和の単位元と呼ばれる。
×: R²→R¹は積と呼ばれる２項演算。
I: R⁰→R¹は積の単位元と呼ばれる０項演算。

また、半環は次の公理を持つ（0項演算の関数適用は省略して書いている）。

和は可換モノイド
- 交換律：∀a,b∈R, a＋b = b＋a
- 結合律：∀a,b,c∈R, (a＋b)＋c = a＋(b＋c)
- 単位律：∀a∈R, O＋a = a = a＋O
積はモノイド
- 結合律：∀a,b,c∈R, (a×b)×c = a×(b×c)
- 単位律：∀a∈R, I×a = a = a×I
部分適用された積は、和の準同型写像（自己準同型）
- 左分配律（積の左作用は和を保存する）：∀f,a,b∈R, f×(a＋b) = (f×a)＋(f×b)
- 右分配律（積の右作用は和を保存する）：∀a,b,f∈R, (a＋b)×f = (a×f)＋(b×f)
- ゼロ化（積の左右の作用は和の単位元を保存する）：∀f∈R, f×O = O = O×f

半環と整合する図

次のそれぞれの図を象形文字I, X, ⅄, ꓕ, Y, T, [f]で書き表すことにする。

各図は上下に端点を持つ、上の端点を項数（arity）、下の端点を余項数（co_arity）と呼ぶことにする。表としてまとめれば、次のようになる。

図	項数	余項数
I	1	1
X	2	2
⅄	1	2
ꓕ	1	0
Y	2	1
T	0	1
[f]	1	1

図の並列合成

図の並列合成を⊗で表すことにする。すなわち、任意の図F、Gについて、Fを左に描き、Gを右に描くとき、これをF⊗Gと書く。図から明らかなように、F⊗Gの項数はFの項数とGの項数の和になる（余項数についても同様）。

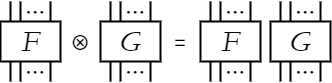
図の直列合成

図の直列合成を;で表すことにする。すなわち、任意の図F、Gについて、Fの余項数とGの項数が一致し、Fを上に描き、Gを下に描くとき、これをF;Gと書く。図から明らかなように、F;Gの項数はFの項数と等しく、F;Gの余項数はGの余項数と等しい。

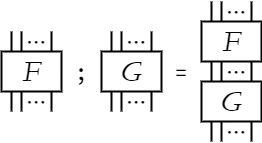
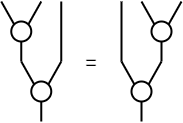
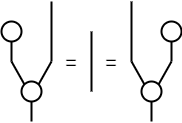
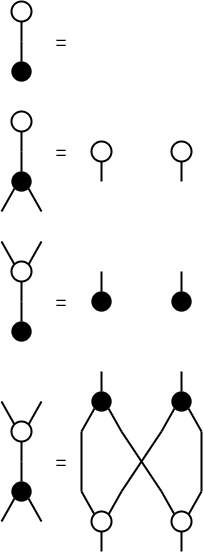
図の可換モノイド

合流Y,Tが次の３つの公理を満たす可換モノイドであるとしよう。これは、半環の和をYに割り当て、半環の和の単位元をTに割り当てれば満たせる。なお、図には変数が現れないので、次の式はポイントフリースタイルで書かれているとも言える。可換モノイドの公理としては見慣れない式だが、図としてはとても単純な図の変形である。そして、この記事における図の変形規則を受け入れることさえできれば、それで充分であろう。（なぜ可換モノイドを考えるのかと言えば、0本以上の合流を1点にまとめて描けるようにするためだが、天下り的に受け入れてもよいのではなかろうか）。

交換律：X;Y = Y
結合律：(Y⊗I);Y = (I⊗Y);Y
単位律：(T⊗I);Y = I = (I⊗T);Y

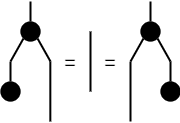
図の余可換余モノイド

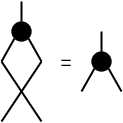
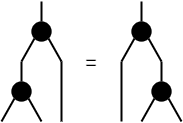
また、分岐⅄,ꓕについて、次の３つの公理を満たす余可換余モノイドであるとしよう。これは、値の複製を⅄に割り当て、値の破棄をꓕに割り当てれば満たせる。図としては可換モノイドの図の変形を上下反転して、丸の白黒を反転しただけである。そして、そのような認識で十分であろう。

余交換律：⅄;X = ⅄
余結合律：⅄;(⅄⊗I) = ⅄;(I⊗⅄)
余単位律：⅄;(ꓕ⊗I) = I = ⅄;(I⊗ꓕ)

図の自己準同型

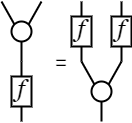
さらに、変換[f]について、合流Y,Tと分岐⅄,ꓕを保存するとしよう。これは、半環の積による右作用（or左作用）を[f]に割り当てればよい。

Y;[f] = ([f]⊗[f]);Y
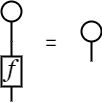
T;[f] = T
[f];⅄ = ⅄;([f]⊗[f])
[f];ꓕ = ꓕ

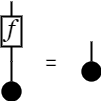
図の計算

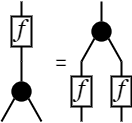
半環の和をYに、半環の和の単位元をTに、半環の積による右作用を[f]に割り当てるとき、次が成り立つ。ただし、＋も半環の和であり、×は半環の積を表す。

⅄;([f]⊗[g]);Y = [f＋g]
[f];[g] = [f×g]

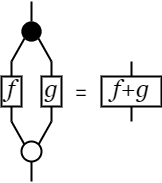
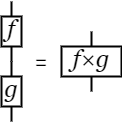
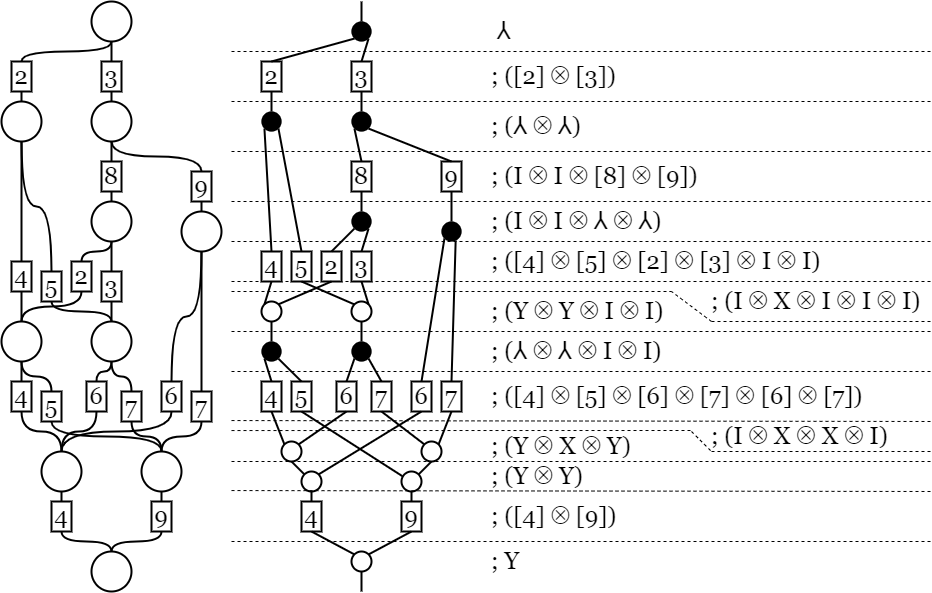
最初に見てきた図は、これらの変形によって計算できる。具体的な手順としては次のようになる。

変換が分岐（や合流）を保存することを利用し、変換を分配し、連続する分岐（や合流）を作る。
その際に変換が連続した場合は積を計算する。
そして連続する分岐（や合流）が結合律（余結合律）と交換律（余交換律）で結線を付け替えられることを利用し、分岐と合流で挟まれた２つの変換を作る。
分岐と合流で挟まれた２つの変換の和を計算する。
結果として変換が連続した場合は積を計算する。
以上の操作ができなくなるまで操作を繰り返す。

例えば、大きな白丸を分岐と合流へ適切に置き換えれば、パターンの数え上げを次のように計算できる。その計算結果「12899」は、確かに元の図の計算結果と一致している。

その他の図の等式変形

なお、図の等式変形としては次のようなものもある（上の計算でも暗黙的に使っている）。

結線の伸び縮み
- I;I=I
- (I⊗I);X=X=X;(I⊗I)
- I;⅄=⅄=⅄;(I⊗I)
- I;ꓕ=ꓕ
- (I⊗I);Y=Y=Y;I
- T=T;I
- I;[f]=[f]=[f];I

交差のすり抜け
- X;X=I⊗I
- X;(⅄⊗I)=(I⊗⅄);(X⊗I);(I⊗X)
- X;(I⊗⅄)=(⅄⊗I);(I⊗X);(X⊗I)
- X;(ꓕ⊗I)=I⊗ꓕ
- X;(I⊗ꓕ)=ꓕ⊗I
- (Y⊗I);X=(I⊗X);(X⊗I);(I⊗Y)
- (I⊗Y);X=(X⊗I);(I⊗X);(Y⊗I)
- (T⊗I);X=I⊗T
- (I⊗T);X=T⊗I
- ([f]⊗I);X=X;(I⊗[f])
- (I⊗[f]);X=X;([f]⊗I)

白黒
- T;ꓕ= （右辺は空の図を意味する。つまり、いつでもどこからでも図からT;ꓕを除去できる）
- T;⅄=T⊗T
- Y;ꓕ=ꓕ⊗ꓕ
- Y;⅄=⅄;(I⊗X⊗I);Y

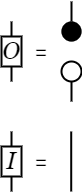
単位元の積
- [O]=ꓕ;T
- [I]=I

関数

上で見た通り、図の変形によって直接計算できるが、直感的に変換は関数のように見える。実際、図は具体的な関数として解釈できる。このことをPythonのコードによって示しておこう。ただし、演算子オーバーロードで使用可能な記号の関係で、下表のとおり⊗を+、;を*と表記している。

図	Python上の関数名	定義の簡易的な説明
I	`id`	`id([x])`=`[x]`
X	`swap`	`swap([x,y])`=`[y,x]`
⅄	`copy`	`copy([x])`=`[x,x]`
ꓕ	`discard`	`discard([x])`=`[]`
Y	`add`	`add([x,y])`は`x`と`y`の和
T	`zero`	`zero([])`は和の単位元
[f]	`mul(f)`	`mul(y)(x)`は`x`と`y`の積
F⊗G	`F + G`	`(F + G)(xs)`は引数`xs`を`F`と`G`で分け合って、それぞれの計算結果のリストを連接する
F;G	`F * G`	`(F * G)(xs)`=`G(F(xs))`

関数表現による計算（Python）

from typing import Callable, Generic, TypeVar
from dataclasses import dataclass


R = TypeVar("R")


@dataclass(frozen=True)
class Rig(Generic[R]):
    add: Callable[[R, R], R]
    zero: R
    mul: Callable[[R, R], R]
    one: R


rig_type = int
rig = Rig[rig_type](
    lambda x, y: x + y,
    0,
    lambda x, y: x * y,
    1,
)


@dataclass(frozen=True)
class Fun(Generic[R]):
    rig: Rig[R]
    arity: int
    co_arity: int
    call: Callable[[list[R]], list[R]]

    def __call__(self: "Fun", xs: list[R]) -> list[R]:
        assert len(xs) == self.arity
        ys = self.call(xs)
        assert len(ys) == self.co_arity
        return ys

    def __add__(self: "Fun[R]", other: "Fun[R]") -> "Fun[R]":
        assert self.rig == other.rig
        return Fun(
            self.rig,
            self.arity + other.arity,
            self.co_arity + other.co_arity,
            lambda xs: self(xs[: self.arity]) + other(xs[self.arity :]),
        )

    def __mul__(self: "Fun[R]", other: "Fun[R]") -> "Fun[R]":
        assert self.rig == other.rig
        assert self.co_arity == other.arity
        return Fun(
            self.rig,
            self.arity,
            other.co_arity,
            lambda xs: other(self(xs)),
        )


id = Fun[rig_type](rig, 1, 1, lambda xs: [xs[0]])
swap = Fun[rig_type](rig, 2, 2, lambda xs: [xs[1], xs[0]])
copy = Fun[rig_type](rig, 1, 2, lambda xs: [xs[0], xs[0]])
discard = Fun[rig_type](rig, 1, 0, lambda _: [])
add = Fun[rig_type](rig, 2, 1, lambda xs: [rig.add(xs[0], xs[1])])
zero = Fun[rig_type](rig, 0, 1, lambda _: [rig.zero])


def mul(f: rig_type) -> Fun[rig_type]:
    return Fun(rig, 1, 1, lambda xs: [rig.mul(xs[0], f)])


compound = (
    copy
    * (mul(2) + mul(3))
    * (copy + copy)
    * (id + id + mul(8) + mul(9))
    * (id + id + copy + copy)
    * (mul(4) + mul(5) + mul(2) + mul(3) + id + id)
    * (id + swap + id + id + id)
    * (add + add + id + id)
    * (copy + copy + id + id)
    * (mul(4) + mul(5) + mul(6) + mul(7) + mul(6) + mul(7))
    * (id + swap + swap + id)
    * (add + swap + add)
    * (add + add)
    * (mul(4) + mul(9))
    * add
)

print(compound([rig.one]))  # => [12899]

from typing import Callable, Generic, TypeVar

from dataclasses import dataclass

R = TypeVar("R")

@dataclass(frozen=True)

class Rig(Generic[R]):

add: Callable[[R, R], R]

zero: R

mul: Callable[[R, R], R]

one: R

rig_type = int

rig = Rig[rig_type](

lambda x, y: x + y,

lambda x, y: x * y,

)

@dataclass(frozen=True)

class Fun(Generic[R]):

rig: Rig[R]

arity: int

co_arity: int

call: Callable[[list[R]], list[R]]

def __call__(self: "Fun", xs: list[R]) -> list[R]:

assert len(xs) == self.arity

ys = self.call(xs)

assert len(ys) == self.co_arity

return ys

def __add__(self: "Fun[R]", other: "Fun[R]") -> "Fun[R]":

assert self.rig == other.rig

return Fun(

self.rig,

self.arity + other.arity,

self.co_arity + other.co_arity,

lambda xs: self(xs[: self.arity]) + other(xs[self.arity :]),

)

def __mul__(self: "Fun[R]", other: "Fun[R]") -> "Fun[R]":

assert self.rig == other.rig

assert self.co_arity == other.arity

return Fun(

self.rig,

self.arity,

other.co_arity,

lambda xs: other(self(xs)),

)

id = Fun[rig_type](rig, 1, 1, lambda xs: [xs[0]])

swap = Fun[rig_type](rig, 2, 2, lambda xs: [xs[1], xs[0]])

copy = Fun[rig_type](rig, 1, 2, lambda xs: [xs[0], xs[0]])

discard = Fun[rig_type](rig, 1, 0, lambda _: [])

add = Fun[rig_type](rig, 2, 1, lambda xs: [rig.add(xs[0], xs[1])])

zero = Fun[rig_type](rig, 0, 1, lambda _: [rig.zero])

def mul(f: rig_type) -> Fun[rig_type]:

return Fun(rig, 1, 1, lambda xs: [rig.mul(xs[0], f)])

compound = (

copy

* (mul(2) + mul(3))

* (copy + copy)

* (id + id + mul(8) + mul(9))

* (id + id + copy + copy)

* (mul(4) + mul(5) + mul(2) + mul(3) + id + id)

* (id + swap + id + id + id)

* (add + add + id + id)

* (copy + copy + id + id)

* (mul(4) + mul(5) + mul(6) + mul(7) + mul(6) + mul(7))

* (id + swap + swap + id)

* (add + swap + add)

* (add + add)

* (mul(4) + mul(9))

* add

)

print(compound([rig.one])) # => [12899]

なお、compoundの式は、輪切りにした図のそれぞれを並列合成し、それらを順に直列合成することで導出される。

行列

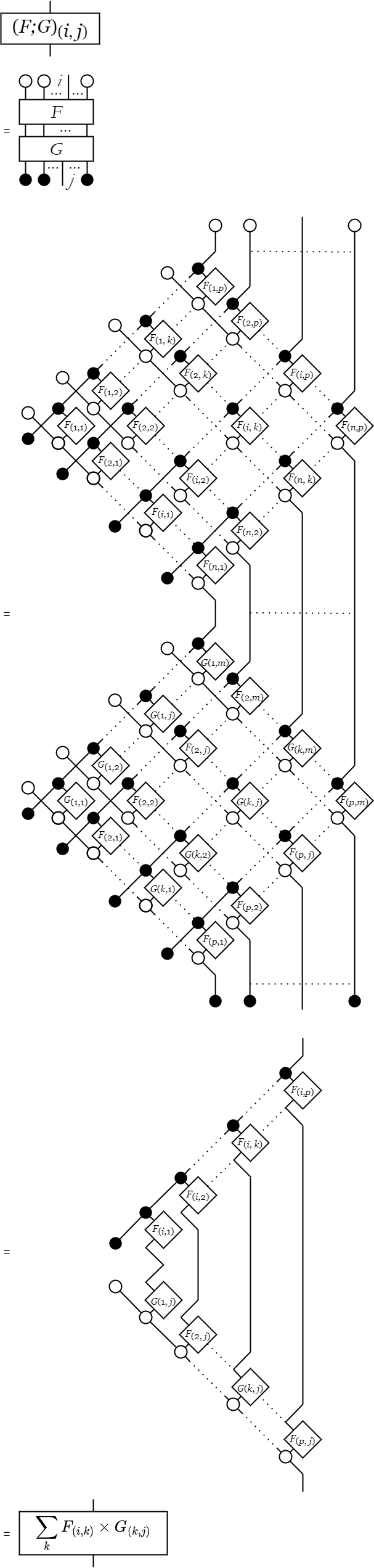
次図のようにn×m個の変換を並べて、規則的に結線できる。つまり任意の行列から、対応した図が作れる。ただし、行列と対応する図にどのような意味があるかは、これだけではわからない。

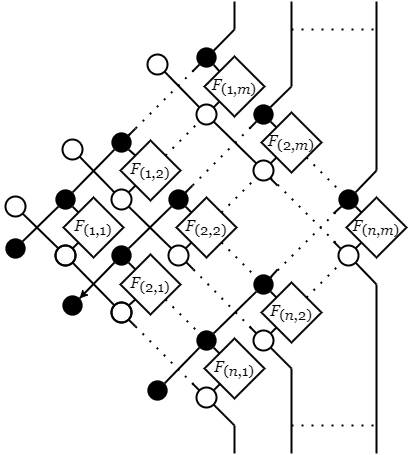
行列要素

行列Fの図のi番目以外のすべての入力をTで閉じ、j番目以外のすべての出力をꓕで閉じてみる。すると、下図のように行列Fのi,j要素のみが取り出せる。

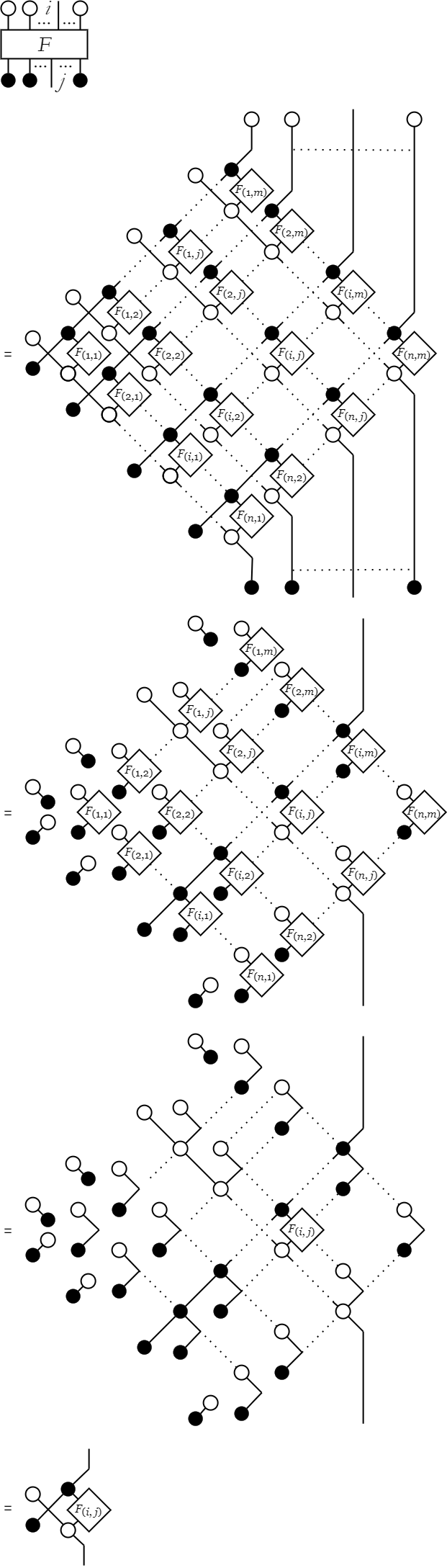
基本図の行列

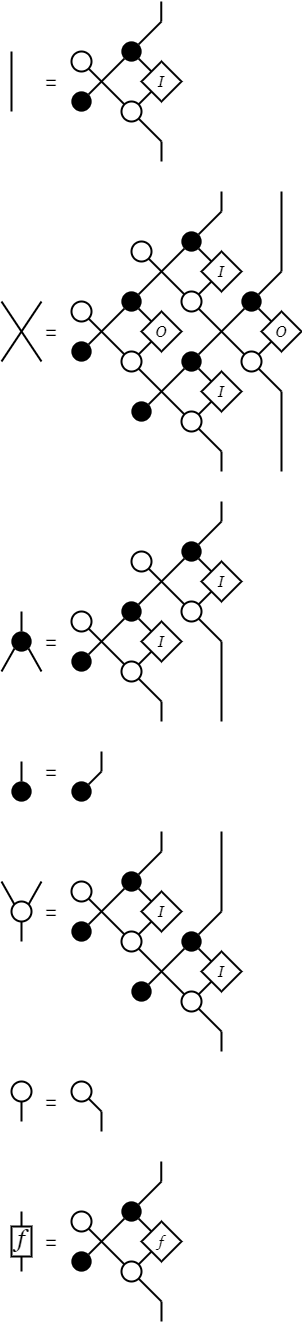
逆に言えば、行列として表現可能な図はi番目以外の入力とj番目以外の出力を閉じれば、i,j要素が取得できる。この考えを適用すると、基本的な図と行列の対応は下表のようになる。ただし、行列は行ベクトルを並べたものとして表記する。また、行列の成分としてのIは積の単位元であり、Oは和の単位元である。

図	行列	定義の簡易的な説明
I	`[[I]]`	1次の単位行列
X	`[[O,I],[I,O]]`
⅄	`[[I,I]]`	積の単位元のみからなる1×2行列
ꓕ	`[[]]`	1×0行列
Y	`[[I],[I]]`	積の単位元のみからなる2×1行列
T	`[]`	0×1行列
[f]	`[[f]]`	値fのみからなる1×1行列

図に起こせば、次のような等式になる。これが正しく成立しているかは、線をなぞれば確かめられよう。ただし、変換[O]は断線を表し、変換[I]は結線を表すと考えた方が確かめやすい。

行列の並列合成

では、並列合成F⊗Gはどのように考えればよいだろうか。FとGがお互いに干渉しないこと、つまり断線していることを加味すれば、行列Fと行列Gのブロック対角行列として理解できる。ここで言うブロック対角行列は、FとGの要素からなるブロックを対角線上に並べた行列[[F, O],[O, G]]を意図している（Oはゼロ行列）。このことは次のような図の変形を考えればわかる。

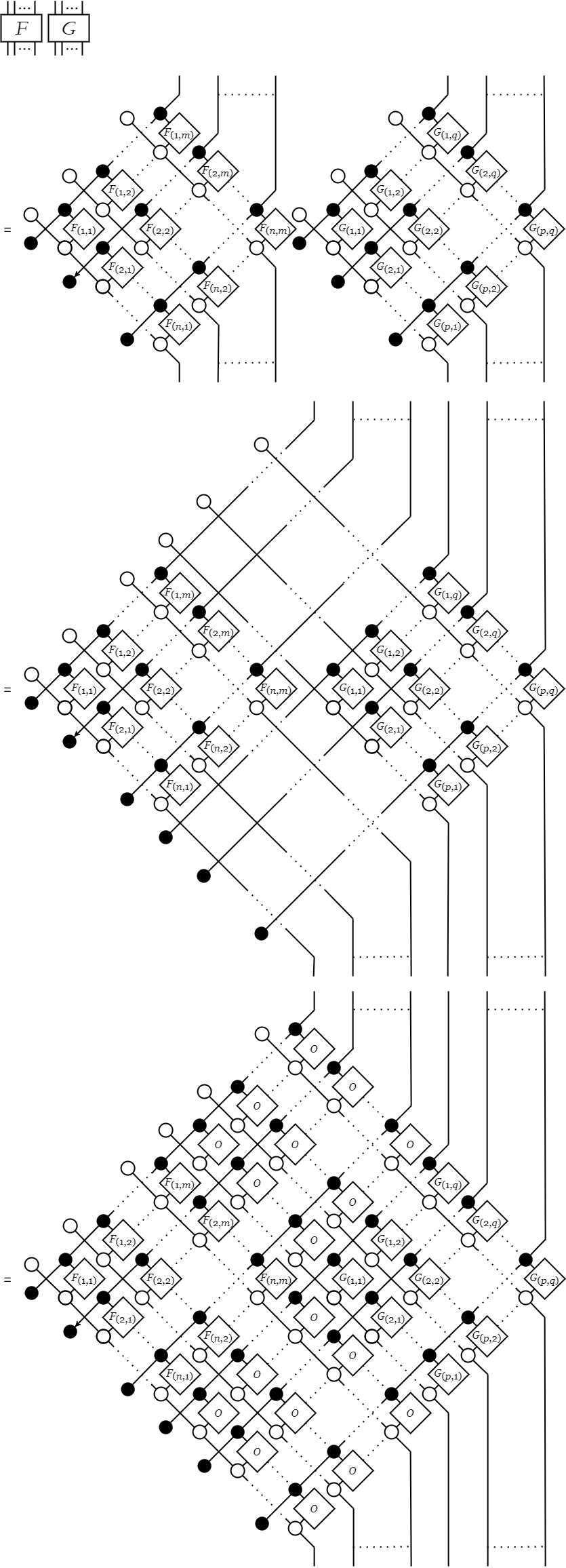
行列の直列合成

次に直列合成F;Gは行列Fと行列Gの行列積として理解できる。このことは成分ごとの図の変形を考えればわかる。

行列表現による計算（Python）

以上を踏まえ、Pythonのコード（２次元のリスト）によって計算してみよう。ただし、行列のブロック対角行列を+、行列積を*と表記している。

from typing import Callable, Generic, TypeVar
from dataclasses import dataclass
from functools import reduce


R = TypeVar("R")


@dataclass(frozen=True)
class Rig(Generic[R]):
    add: Callable[[R, R], R]
    zero: R
    mul: Callable[[R, R], R]
    one: R


rig_type = int
rig = Rig[rig_type](
    lambda x, y: x + y,
    0,
    lambda x, y: x * y,
    1,
)


@dataclass(frozen=True)
class Mat(Generic[R]):
    rig: Rig[R]
    arity: int
    co_arity: int
    matrix: list[list[R]]

    def is_valid(self: "Mat") -> bool:
        return (
            all(len(row) == self.co_arity for row in self.matrix)
            and len(self.matrix) == self.arity
        )

    def __add__(self: "Mat", other: "Mat") -> "Mat":
        assert self.rig == other.rig
        assert self.is_valid() and other.is_valid()
        rig = self.rig
        arity = self.arity + other.arity
        co_arity = self.co_arity + other.co_arity
        m1 = [row + ([rig.zero] * other.co_arity) for row in self.matrix]
        m2 = [([rig.zero] * self.co_arity) + row for row in other.matrix]
        matrix = m1 + m2
        return Mat(rig, arity, co_arity, matrix)

    def __mul__(self: "Mat", other: "Mat") -> "Mat":
        assert self.rig == other.rig
        assert self.is_valid() and other.is_valid()
        assert self.co_arity == other.arity
        rig = self.rig
        arity = self.arity
        co_arity = other.co_arity

        if self.co_arity == 0:
            matrix = [[rig.zero] * co_arity] * arity
            return Mat(rig, arity, co_arity, matrix)

        table = [
            [
                reduce(rig.add, [rig.mul(x, y) for x, y in zip(row, col)], rig.zero)
                for col in zip(*other.matrix)
            ]
            for row in self.matrix
        ]
        return Mat(rig, arity, co_arity, table)


id = Mat[rig_type](rig, 1, 1, [[rig.one]])
swap = Mat[rig_type](rig, 2, 2, [[rig.zero, rig.one], [rig.one, rig.zero]])
copy = Mat[rig_type](rig, 1, 2, [[rig.one, rig.one]])
discard = Mat[rig_type](rig, 1, 0, [[]])
add = Mat[rig_type](rig, 2, 1, [[rig.one], [rig.one]])
zero = Mat[rig_type](rig, 0, 1, [])


def mul(f: rig_type) -> Mat[rig_type]:
    return Mat(rig, 1, 1, [[f]])


compound = (
    copy
    * (mul(2) + mul(3))
    * (copy + copy)
    * (id + id + mul(8) + mul(9))
    * (id + id + copy + copy)
    * (mul(4) + mul(5) + mul(2) + mul(3) + id + id)
    * (id + swap + id + id + id)
    * (add + add + id + id)
    * (copy + copy + id + id)
    * (mul(4) + mul(5) + mul(6) + mul(7) + mul(6) + mul(7))
    * (id + swap + swap + id)
    * (add + swap + add)
    * (add + add)
    * (mul(4) + mul(9))
    * add
)

print(compound.matrix[0][0])  # => 12899

100

101

102

from typing import Callable, Generic, TypeVar

from dataclasses import dataclass

from functools import reduce

R = TypeVar("R")

@dataclass(frozen=True)

class Rig(Generic[R]):

add: Callable[[R, R], R]

zero: R

mul: Callable[[R, R], R]

one: R

rig_type = int

rig = Rig[rig_type](

lambda x, y: x + y,

lambda x, y: x * y,

)

@dataclass(frozen=True)

class Mat(Generic[R]):

rig: Rig[R]

arity: int

co_arity: int

matrix: list[list[R]]

def is_valid(self: "Mat") -> bool:

return (

all(len(row) == self.co_arity for row in self.matrix)

and len(self.matrix) == self.arity

)

def __add__(self: "Mat", other: "Mat") -> "Mat":

assert self.rig == other.rig

assert self.is_valid() and other.is_valid()

rig = self.rig

arity = self.arity + other.arity

co_arity = self.co_arity + other.co_arity

m1 = [row + ([rig.zero] * other.co_arity) for row in self.matrix]

m2 = [([rig.zero] * self.co_arity) + row for row in other.matrix]

matrix = m1 + m2

return Mat(rig, arity, co_arity, matrix)

def __mul__(self: "Mat", other: "Mat") -> "Mat":

assert self.rig == other.rig

assert self.is_valid() and other.is_valid()

assert self.co_arity == other.arity

rig = self.rig

arity = self.arity

co_arity = other.co_arity

if self.co_arity == 0:

matrix = [[rig.zero] * co_arity] * arity

return Mat(rig, arity, co_arity, matrix)

table = [

[

reduce(rig.add, [rig.mul(x, y) for x, y in zip(row, col)], rig.zero)

for col in zip(*other.matrix)

]

for row in self.matrix

]

return Mat(rig, arity, co_arity, table)

id = Mat[rig_type](rig, 1, 1, [[rig.one]])

swap = Mat[rig_type](rig, 2, 2, [[rig.zero, rig.one], [rig.one, rig.zero]])

copy = Mat[rig_type](rig, 1, 2, [[rig.one, rig.one]])

discard = Mat[rig_type](rig, 1, 0, [[]])

add = Mat[rig_type](rig, 2, 1, [[rig.one], [rig.one]])

zero = Mat[rig_type](rig, 0, 1, [])

def mul(f: rig_type) -> Mat[rig_type]:

return Mat(rig, 1, 1, [[f]])

compound = (

copy

* (mul(2) + mul(3))

* (copy + copy)

* (id + id + mul(8) + mul(9))

* (id + id + copy + copy)

* (mul(4) + mul(5) + mul(2) + mul(3) + id + id)

* (id + swap + id + id + id)

* (add + add + id + id)

* (copy + copy + id + id)

* (mul(4) + mul(5) + mul(6) + mul(7) + mul(6) + mul(7))

* (id + swap + swap + id)

* (add + swap + add)

* (add + add)

* (mul(4) + mul(9))

* add

)

print(compound.matrix[0][0]) # => 12899

おわりに

さて、この記事は半環と図の相性の良さについて垣間見ることを目標としていたのであった。図というのは、より明確に言えば半環の値を重みとして持つDAG（有向非巡回グラフ）のことだ。

記事の最初に見たのは、DAGの辺の重みを半環の積、頂点での合流を半環の有限和、頂点からの分岐を有限複製と捉えれば、DAGに制限されたダイクストラ法のように計算できるということであった。ここで重要な点は、半環を取り替えるだけで、図たるDAGをさまざまに解釈（計算）できるという事実だ。

次に、半環と整合する図としてI, X, ⅄, ꓕ, Y, T, [f]の基本図形と、水平合成⊗と垂直合成;を導入した。そして、重み付きDAGを分解、再構築し、図として計算できることを見た。また、I, X, ⅄, ꓕ, Y, T, [f]に関数表現を与え、⊗と;に相当する関数合成を定義することで、関数として計算できることも見た。最後に、行列表現も与え、⊗と;に相当する行列演算を使うことで、行列として計算できることも見た。

図を関数や行列として捉え直す視点が得られただろうか。もしも、ここまで読み切ったのなら、あなたが何気なく描いた図に概算値でも半環の値を載せてみてほしい。そうすれば、図から想像だにしなかった解釈（計算結果）が得られるかもしれない。

おまけのこぼれ話

圏

この記事で扱ったようなグラフィカル言語は圏論を背景に持つ。ただ、個別の図を計算するだけであれば圏論の知識は不要なので、本編では言及しなかった。その点を含めて、あるいは線形代数との関係をより深く知りたい場合は、グラフィカル線形代数をおススメする。なお、関数と行列による表現という文言を見て、量子力学（波動力学と行列力学）を想起してしまった人は圏論的量子力学について調べることをおススメする。

計算順序

この記事では最初、上から下へ丸い頂点を埋めるように計算を進めていった。そのため、計算順序が上から下へ縛られているかのように錯覚しただろうか。しかし、行列積として計算できること思い出せば、行列積の結合律「(A*B)*C=A*(B*C)」より（あるいは圏の結合律より）、実際にはどこから計算しても良いことがわかる。上からでも、下からでも、真ん中からでもよく、計算の順番に制限はない。

ループと方程式

この記事では下から上へ戻るようなループ結線は許容しなかったが、そのような結線を許容すると信号流れ図(signal-flow graph; SFG)になる。ループを理解する方法の１つは、図を連立１次方程式と解釈することだ。というのも、任意の関数が逆関数を持つとは限らないため、関数を上下逆転させるには、関数を関係（左全域性と右一意性を満たす二項関係）と捉え直して、逆関係を考える必要が出てくる。関係として捉え直せば、図の計算結果は全体の関係を満たす値の集合に違いない。いくつかの連立した関係式を満たす値の集合とは、すなわち方程式の解である。

なお、方程式以外にも、量子回路のようにユニタリ変換（可逆な変換）のみを考えてもよいだろう。あるいは、無限和のような結びを備えた単位的クオンテール（Unital Quantale）を考える、など。トレース付きモノイダル圏やコンパクト閉圏の応用は興味深そうである。

Where would a wise man hide a leaf?

最初に見ていった図の空欄の丸を状態と捉えるなら、四角い箱は行動に伴うなんらかの利得や費用になる。重みを付与する前の概念図を眺めていると、ゼロコストで物事が進むように錯覚してしまうことがある。しかも、それが論理的帰結として成り立つような気さえしてくる。しかし、ゼロコストを想定して描いた図とは、すなわちゼロ環を想定していることになり、結果は自明なゼロにしかならない。つまり、何も得られないということが行動の前、計画の時点で約束される。

自由な半環

よく知られたいくつかの抽象データ型から半環を作れる。

有限リスト（list, 自由モノイド）
有限多重集合(bag, 自由可換モノイド)
有限集合(set, 自由冪等可換モノイド)

外側をbagかset、内側を３つのうちのいずれかにすれば、半環を作れる。例えば、型Tについて、set[list[T]]という型を考える。このとき、和を２つの集合の合併、和の単位元を空集合、積の単位元を空列のみからなる単元集合とし、積を２つの集合の要素列どうしの連接とすれば、これは半環になる。この半環を計算すると、選言標準形のようなものが得られる。

ただ、プログラミング言語によってはset[list[T]]は許容されないこともある。 Pythonではlist[T]がハッシュ化できないため、set[list[T]]の値を構築しようとしても例外が発生する。この点を無視して、set[list[T]]の半環をPython風の疑似コードで書いてみると、次のようになる。

def add(xss: set[list[T]], yss: set[list[T]]) -> set[list[T]]:
  return xss | yss

zero: set[list[T]] = set([])

def mul(xss: set[list[T]], yss: set[list[T]]) -> set[list[T]]:
  return set([xs + ys for xs in xss for ys in yss])

one: set[list[T]] = set([[]])

def add(xss: set[list[T]], yss: set[list[T]]) -> set[list[T]]:

return xss | yss

zero: set[list[T]] = set([])

def mul(xss: set[list[T]], yss: set[list[T]]) -> set[list[T]]:

return set([xs + ys for xs in xss for ys in yss])

one: set[list[T]] = set([[]])

値が関数になる半環

行列で計算できるなら、すべて行列で計算すればよいと思われるだろうか。ただ、値が関数になるような半環を考えるときは、行列よりも関数合成として扱う方が素直な気もする。値が関数になるような半環とは、例えば、任意の可換モノイド(M,＋,O)の自己準同型の集合End(M)が、そのような半環になる。

和：点ごとの和「(f＋g)(x)=f(x)＋g(x)」
和の単位元：常にゼロを返すゼロ写像「O(x)=O」
積：関数合成「(f×g)(x)=g(f(x))」
積の単位元：恒等写像「I(x)=x」

あるいは半環(R,＋,O,×,I)が与えられたとき、点ごとの和と積を考えれば、任意の集合Sの値をRへ送る写像の全体R^S（配置集合）は半環になる。このような半環R^Sは、例えばSに時刻の集合を取れば、時刻ごとに値が変わる動的な図の計算を表せる。

和：点ごとの和「(f＋g)(x)=f(x)＋g(x)」
和の単位元：「O(x)=O」
積：点ごとの積「(f×g)(x)=f(x)×g(x)」
積の単位元：「I(x)=I」

行列のべき乗

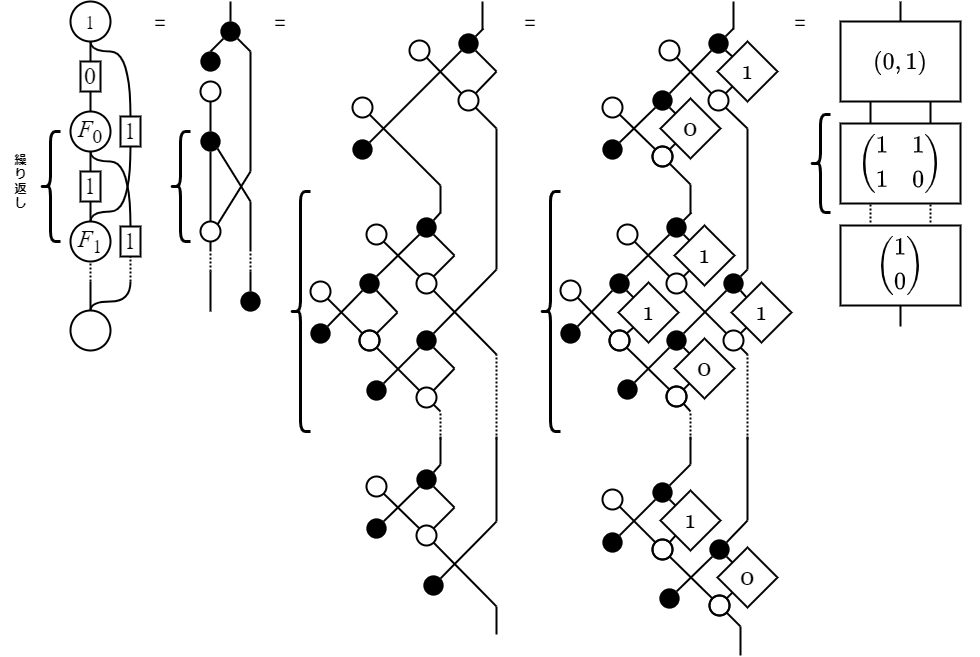
図の中にまったく同じ図の繰り返しが現れる場合、行列のべき乗として計算できる。そして、行列のべき乗は繰り返し二乗法で計算すると効率よく計算できる。もしもその行列を対角化できるようであれば、さらに効率よく計算できる。

例えばフィボナッチ数列がそのような繰り返し構造を持つ。下図はフィボナッチ数列が行列のべき乗で計算できることを表している。（ここからさらに対角化すればフィボナッチ数列の一般項が出てくる）。

その他の半環

英語版のWikipediaが詳しい。

shunki

図の解釈を取り替える

パターンの数え上げ

最大パターン

最小パターン

最長と最短

最大と最小

orとand

ゼロ環

半環

半環と整合する図

図の並列合成

図の直列合成

図の可換モノイド

図の余可換余モノイド

図の自己準同型

図の計算

その他の図の等式変形

関数

関数表現による計算（Python）

行列

行列要素

基本図の行列

行列の並列合成

行列の直列合成

行列表現による計算（Python）

おわりに

おまけのこぼれ話

圏

計算順序

ループと方程式

Where would a wise man hide a leaf?

自由な半環

値が関数になる半環

行列のべき乗

その他の半環

おすすめ

gcloudコマンドで Container Registry から Artifact Registry に移行する

ローカルからCloud SQLに接続する方法 by Cloud SQL Auth Proxy

AnsibleでAlmaLinux 8のGPG keyをインポート出来ない