[社内統計学勉強会]検定と推定

GMOアドマーケティングのエンジニアS.Yです。
前回に引き続き、第3回目の統計勉強会を実施し、検定と推定について学びました。
主に検定をテーマに紹介したいと思います。

1 検定

検定とは、母集団分布の母数に関する仮説をサンプルから検証する統計学的方法です。
母数とサンプルのイメージは視聴率を考えるとわかりやすいかもしれません。
関東では全部で1800万世帯いますが、900世帯をランダムに抽出し、計測器を設置して視聴率を取得しているそうです。
ここでいう関東全体の1800万世帯が母数で、900世帯がサンプルです。
母数である1800万世帯の視聴率を計測できれば話は早いのですが、これが難しいため、母数1800万世帯の視聴率をサンプル900世帯のデータから予測しています。
データの取れない母数1800万世帯の視聴率に対して仮説をたてる場合、検定の方法を使うことで、サンプル900世帯のデータをもとに仮説が正しいか間違っているかを検証して結論を出すことができます。

参考 | ビデオリサーチ視聴率調査方法

2 推定

推定は母数がどのような値になっているかサンプルをもとに具体的な数値で示す手法となっています。
点推定と区間推定があり、点推定は未知の母数の値(θ)をデータから推測し、区間推定はデータから未知の母数の値(θ)の範囲を推測する手法です。
先ほどの視聴率の例ですと、点推定はサンプルをもとに視聴率10％と具体的に決めることで、区間推定はサンプルをもとに視聴率9〜11%と実際に含まれる範囲を推定します。
今回は検定についての記事なので推定についてはふれませんが、こちらも統計の基本的な考え方なので、合わせて覚えておく必要があります。

3 検定手順

それでは例を元に、実際に検定していきましょう。

視聴率は見たか見ていないかになってしまい、今回学んだ範囲とはズレてしまうため、平均視聴時間を例にとって考えて見ます。

NHK放送文化研究所が出している2017年のテレビ平均視聴時間は3時間31分(211分)となっていますが、自分はそんなにテレビを見ていないし、本当はもっと少ないのではないかという疑問を持ったとします。

参考: NHK放送文化研究所 テレビ･ラジオ視聴の現況

このようなケースではどうやって検定していくのでしょうか？

1.仮説

まずは帰無仮説を立てます。
帰無仮説 \(H_0\) : μ=211(分)
対立仮説 \(H_1\) : μ<211

帰無仮説を211分としましたが、ここでは成り立っていないと思われる仮説を設定します。
そして、対立仮説には自分の思っている結果を設定します。今回ですと1日の視聴時間は211分よりも短いと思っているので、\(\mu_0\)<211で表します。
μは母集団平均ですね。
\(H_0\)と\(H_1\)ですが、帰無仮説を英語でNull Hypothesis、対立仮説はAlternative Hypothesisといいます。
HはHypothesisの頭文字、0と1はnull(false)とtrueから取っているのではないかと思います。
なので、\(H_0\)には間違っていると思われる仮説である、\(\mu\)=211分を設定しています。
この\(H_0\)が間違っていると証明できれば、検定できているといえるのではないでしょうか。
\(\mu_0\)が中心の正規分布を考えると、中心から外れるほど\(H_0\)が間違っているといえそうです。

2.判定基準

次に\(H_0\)が間違っていると証明するための基準を決めます。
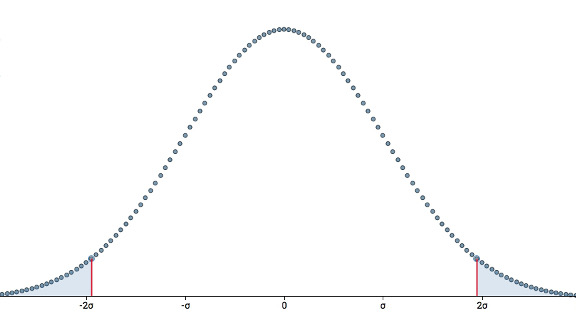
この基準を有意水準といい、αで表します。基本的には0.05か0.01を選択し、正規分布全体の面積を1として考えるので、それぞれ5%と1%です。
上の図のように両側検定だと両端に棄却域があるため、有意水準5%だと右2.5%、左2.5%になります。
この2.5%の面積を数値として表すと1.96で、この数値と次に計算する検定統計量を比較して、\(H_0\)が間違っているかを証明することになります。
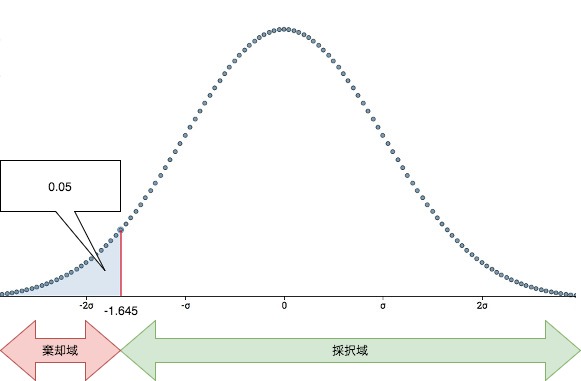
今回は対立仮説\(H_1\)で母平均は本当は低いと考えているため、左側検定となります。
グラフで表すと次のようになり、棄却域は左側のみで5%となります。

3.データの計算

データを取っていきますが、社内でのアンケートなどでは偏ってしまうため、ネットでのランダムなアンケートにするなど偏りが出ないように気をつけます。ネットでのランダムなデータとはいえ、ネットを使っている人という偏った結果になってしまうかもしれませんが、そのような問題をクリアして、次のようなランダムな視聴時間データが集まったとします。

180.3

55.3

190.8

302.2

90.7

203.8

121.5

48.7

179.7

131.6

x̄の分布には次のような性質があるため、標準正規分布として考えることができます。

x̄の分布の標準化から\(u=\frac{\overline{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}\)が\(N(0,1^2)\)に従う

上記の式に代入して、検定統計量\(u_0\)を出してみます。
\(u=\frac{150.46-211}{\sqrt{5935/10}}=-2.484\)

この部分をPythonで書くと次のようになります

4.判定

有意水準5％で、左片側検定の棄却域は-1.645になります。
統計量\(u_0\)=-2.484はこれよりも小さいので、棄却域に含まれることになります。
\(H_0\)の\(\mu=211\)分が間違っていると判断でき、\(H_0\)を棄却することができます。
今回のサンプルアンケートの結果からはテレビ平均視聴時間は3時間31分よりも小さいと結論づけることができます。
サンプルデータで数も少ないため、実際の結果とはなんの関係もありませんが、正しいデータを使うことで、母数を予測することができます。数少ないデータから母数を予測するので、当然間違った結果に至ることがありますが、これを第1種の過誤、第2種の過誤と呼んでいます。
過誤を少なくするために正しいデータを多く取る必要がありそうです。

まとめ

視聴時間を例に実際に検定してみましたが、どうだったでしょうか？
今回使った検定の考え方は統計の基礎的な部分で、この先勉強していく上で大切なことだと思います。
仕事でたまったデータや、自分の毎日の記録など、身近なところでデータを元に仮説を立て、分析していくことでさらに理解が深まると思いますし、新たにデータを取って分析することで、新たな発見があるかもしれません。