【Python】噂の”LightweightMMM”を使ってみた

この記事は GMOアドマーケティング Advent Calendar 2023 21日目の記事です．

はじめに

こんにちは．GMOアドパートナーズにてインターンシップとして参加させていただいております，kantayamaです．現在は修士課程2年で，確率ニューラルネットモデルに関する理論研究をしています．

インターンシップをしていく中で，マーケティング・ミックス・モデリング（MMM）に興味を持ち，まずは実装してみようということで，Googleが公開しているMMMライブラリ「LightweightMMM」を触ってみました．実際に実務で活用するにはより厳密な解析が必要になるかと思いますが，とりあえずMMMの全体像を掴みたいなと思い実装してみたので今回紹介させていただきます．

マーケティング・ミックス・モデリング（MMM）とは

概要

MMMとは，メディア運営や広告掲載など，個々のマーケティング施策がどれだけ成果に影響を与えたのかを統計学を使って定量的に推定する分析手法です．MMMを行うことでマーケティング施策にかかるコストと，それによって生じる利益の関係性を解明して，投資対効果を最大化する最適なマーケティング戦略を考えることができます．MMMの概要を掴む上で，弊社の先輩がMMMとは何かについて記事を書いてくださったのでそちらを読んでから先に進んでいただくとより理解が深まると思いますので是非参照してみてください．

GMOアドパートナーズ TECH BLOG byGMO

広告ROIの鍵！マーケティング・ミックス・モデリング入門

こんにちは、GMO NIKKOのT.Sです。機械学習エンジニアをしております。最近マーケティング業界で注目されているMMM（マーケティング・ミックス・モデル）について調査したので記事に残したいと思います。マーケティング・ミックス・モデリングとは？マーケティング・ミックス・モデリング（MMM）とは、マーケティングに関わる活動（PRやWeb広告）がどれだけ売上やCVに貢献したかを統計的に分析する手法です。MMMの目的としては、マーケティング活動の費用（原因）とそれによって生じた売上（結果）の関係を解明して、費用対効果...

なぜ，今MMMが必要？

今日の世界的な3rd Party Cookie 規制の流れを受け，今後ユーザー個人の行動データに基づいて分析を行うことはより一層難しくなることが予想されます．他方MMMは，Cookieなどを用いた個人の行動データに基づくリアルタイムの分析は行わず，主に広告出稿量（テレビCMのGPR，デジタル広告のインプレッション数，クリック数など）やコスト，成果（売上、申込数・契約数などのコンバージョン数），及び市場環境，季節性，天候といった外部要因に関するデータを使用したマーケティング分析を行います．故に，この「Cookieレス時代」においてもマーケティング活動を正確かつ持続的に測定可能になります．

LightweightMMM

この時代の流れを受け，Meta社のR言語で書かれたRobynや、Google社のPythonで書かれたLightweightMMMなど，多くのビックテック企業が相次いでMMMライブラリを公開しています．今回はこの中でも，世の中で比較的使用率の高い（と思う）PythonのLightweightMMMを，Kaggleで公開されているデータセットを分析する形で紹介させていただきます．

このLightweightMMMは，Jin et al. (2017)の論文をベースにベイジアン非線形時系列モデルを採用したライブラリで，Googleによって2022年に公開されました．モデル内部はnumpyroで実装されていることから，MCMCサンプリングをする際に非常に高速に動作するのが特徴です．

実装

それでは早速，実装に移っていきます．今回はkaggleに良い感じのオープンデータセットが公開されていたので，それを使ってLightweightMMMを体験してみようと思います．予めリンク先のcsvファイルのダウンロードの方を済ませておくと良いと思います．

ライブラリのインポート

まず初めに，今回使用するライブラリを読み込みます．

import jax.numpy as jnp
import numpyro
from lightweight_mmm import lightweight_mmm
from lightweight_mmm import optimize_media
from lightweight_mmm import plot
from lightweight_mmm import preprocessing
from lightweight_mmm import utils
from lightweight_mmm import media_transforms
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.stats.outliers_influence import variance_inflation_factor

import jax.numpy as jnp

import numpyro

from lightweight_mmm import lightweight_mmm

from lightweight_mmm import optimize_media

from lightweight_mmm import plot

from lightweight_mmm import preprocessing

from lightweight_mmm import utils

from lightweight_mmm import media_transforms

import pandas as pd

import matplotlib.pyplot as plt

import numpy as np

import seaborn as sns

from sklearn.linear_model import LinearRegression

from sklearn.metrics import r2_score

from sklearn.metrics import mean_absolute_percentage_error

from statsmodels.stats.outliers_influence import variance_inflation_factor

データの確認

次に，データの確認を行なっていきます．

data = pd.read_csv("Advertising Budget and Sales.csv").drop("Unnamed: 0", axis=1)

1	data = pd.read_csv("Advertising Budget and Sales.csv").drop("Unnamed: 0", axis=1)

時系列プロット

plt.figure(figsize=(18, 5))
plt.plot(data["TV Ad Budget ($)"],  label = "TV Ad Budget (1K$)")
plt.plot(data["Radio Ad Budget ($)"],  label = "Radio Ad Budget (1K$)")
plt.plot(data["Newspaper Ad Budget ($)"],  label = "Newspaper Ad Budget (1K$)")
plt.plot(data["Sales ($)"],  label = "Sales (1M$)")
plt.legend()

plt.figure(figsize=(18, 5))

plt.plot(data["TV Ad Budget ($)"], label = "TV Ad Budget (1K$)")

plt.plot(data["Radio Ad Budget ($)"], label = "Radio Ad Budget (1K$)")

plt.plot(data["Newspaper Ad Budget ($)"], label = "Newspaper Ad Budget (1K$)")

plt.plot(data["Sales ($)"], label = "Sales (1M$)")

plt.legend()

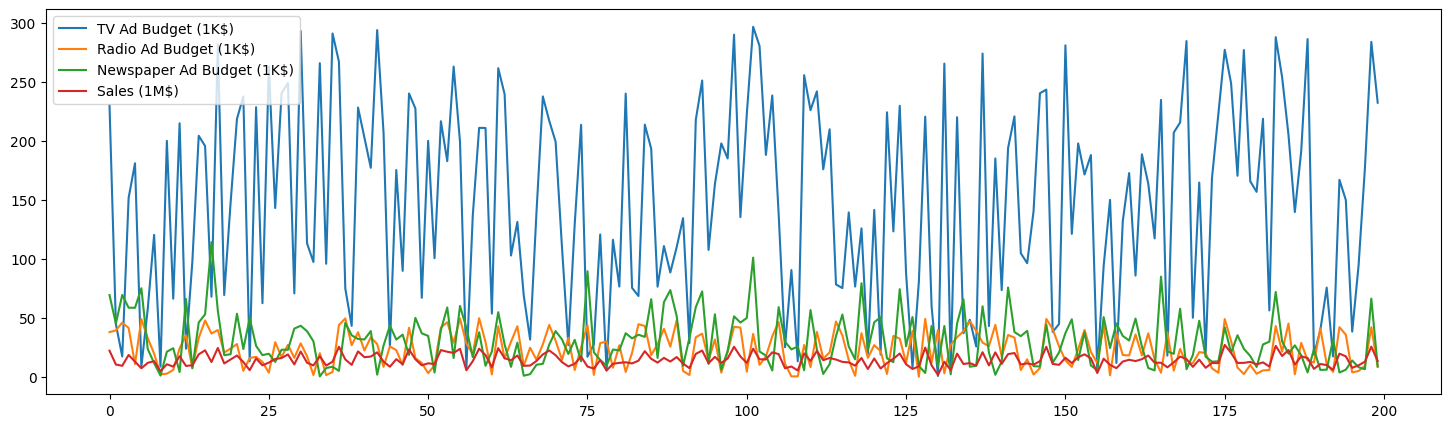
データは”TV”，”Radio”，”Newspaper”の各メディアの広告費と”Sales”からなります．時系列プロットを見てみると，”TV”に対して多くの広告費が投じられている傾向があることがわかります．

※”Sales”は単位が異なる点に注意

共分散混合行列

特徴量間の相関についてみていきましょう．

sns.heatmap(data.corr(), annot=True)

1	sns.heatmap(data.corr(), annot=True)

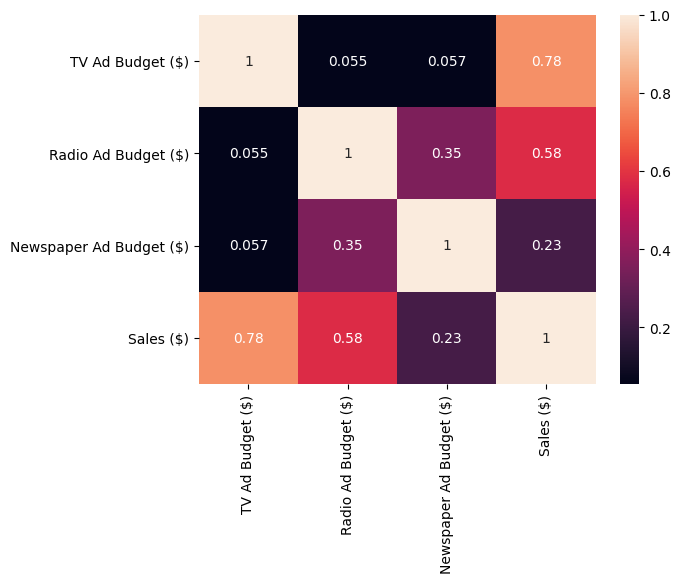
ヒートマップを見てみると各特徴量でわずかに相関が確認されたので，VIFも見て多重共線性の有無を確認してみます．

VIF

media_data = jnp.array(data.iloc[:, :-1])
target = jnp.array(data.iloc[:, -1])
costs = jnp.sum(media_data, axis=0)

media_names = ["TV", "Radio", "Newspaper"]
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(media_data, i) for i in range(media_data.shape[1])]
vif["features"] = media_names

print(vif)

plt.figure(figsize=(12, 3))
plt.bar(vif["features"], vif["VIF Factor"])

media_data = jnp.array(data.iloc[:, :-1])

target = jnp.array(data.iloc[:, -1])

costs = jnp.sum(media_data, axis=0)

media_names = ["TV", "Radio", "Newspaper"]

vif = pd.DataFrame()

vif["VIF Factor"] = [variance_inflation_factor(media_data, i) for i in range(media_data.shape[1])]

vif["features"] = media_names

print(vif)

plt.figure(figsize=(12, 3))

plt.bar(vif["features"], vif["VIF Factor"])

 VIF Factor features<br>0 2.486771 TV<br>1 3.285463 Radio<br>2 3.055244 Newspaper

1	VIF Factor features<br>0 2.486771 TV<br>1 3.285463 Radio<br>2 3.055244 Newspaper

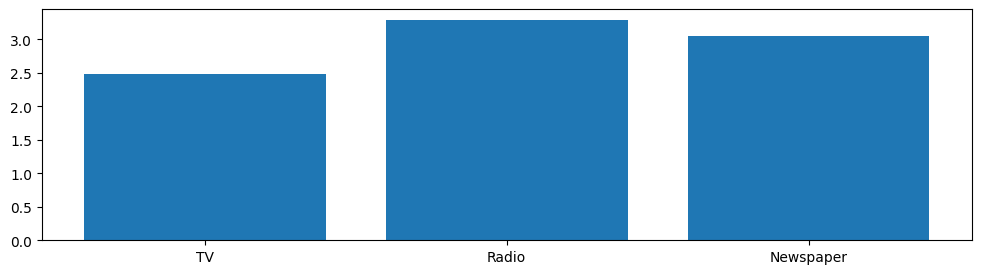
VIF値の結果から，多重共線性の心配はなさそうですね．

前処理

次にモデルの中身についてみていきたいところですが，その前に前処理を行なっていきます．LightweightMMMはMCMCサンプリングによりパラメータの推定を行いますが，その前に各特徴量を平均1に正規化を行うことで，少量の入力データでもモデルが上手く機能することが知られています．またここで学習データとテストデータの分割も行っておきます．今回は後半1/4のデータをテストデータとし，残りを学習データとします．

media_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
target_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)
cost_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)

data_size = data.shape[0]
split_point = data_size - int(data_size / 4)

media_data_train = media_data[:split_point, :]
media_data_test = media_data[split_point: , :]

target_train = target[:split_point]
target_test = target[split_point:]

media_data_train_scale = media_scaler.fit_transform(media_data_train)
target_train_scale = target_scaler.fit_transform(target_train)
media_data_test_scale = media_scaler.fit_transform(media_data_test)
target_test_scale = target_scaler.fit_transform(target_test)
costs_scale = cost_scaler.fit_transform(costs)

plt.figure(figsize=(18, 5))
for i in range(media_data_train.shape[1]):
plt.plot(media_data_train_scale[:, i], label=media_names[i])
plt.plot(target_train_scale, label = "target")
plt.legend()

media_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)

target_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)

cost_scaler = preprocessing.CustomScaler(divide_operation=jnp.mean)

data_size = data.shape[0]

split_point = data_size - int(data_size / 4)

media_data_train = media_data[:split_point, :]

media_data_test = media_data[split_point: , :]

target_train = target[:split_point]

target_test = target[split_point:]

media_data_train_scale = media_scaler.fit_transform(media_data_train)

target_train_scale = target_scaler.fit_transform(target_train)

media_data_test_scale = media_scaler.fit_transform(media_data_test)

target_test_scale = target_scaler.fit_transform(target_test)

costs_scale = cost_scaler.fit_transform(costs)

plt.figure(figsize=(18, 5))

for i in range(media_data_train.shape[1]):

plt.plot(media_data_train_scale[:, i], label=media_names[i])

plt.plot(target_train_scale, label = "target")

plt.legend()

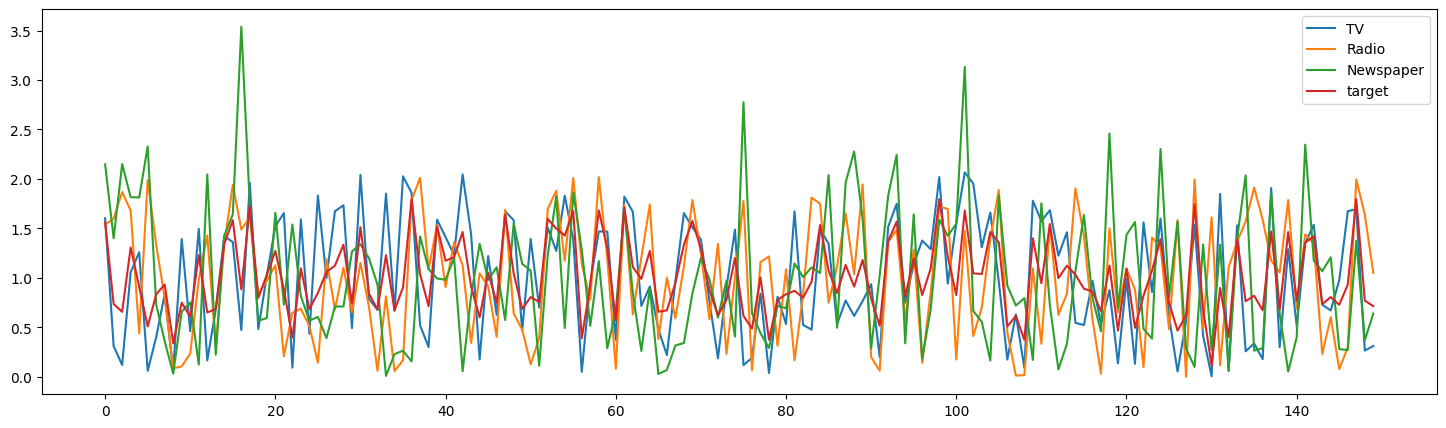
時系列プロットより，正しく正規化できていることが確認できました．

モデル

それでは本題のモデルについて扱っていきます．LightweightMMMは以下のモデルの学習を行います．

KPI(t) = 切片 + トレンド(t) + 季節性(t) + メディア効果(t) + 外部要因(t)

ライブラリ内部で各項の関数が予め定義されており，学習過程において自動的に各項の最適なパラメータを推定します．ここから具体的な各項の形状を確認していきますが，理論的な側面につきましてはJin et al. (2017)か，以下のサイトに非常に分かりやすい解説が記載されていたので，是非参照してみてください．（自分はこの記事が無ければ厳しかったです．笑）

・トレンド

まず初めに記事を元に”トレンド”の形状を見ていきます．

mu = 1 
k_1 = 1.5
k_2 = 0.5
t = np.arange(0, 52*3)

trend_1 = mu * t ** k_1
trend_2 = mu * t ** k_2

plt.figure(figsize=(18, 3))
plt.plot(t, trend_1, label='Trend1')
plt.legend()
plt.show()

plt.figure(figsize=(18, 3))
plt.plot(t, trend_2, label='Trend2', color="Orange")
plt.legend()
plt.show()

mu = 1

k_1 = 1.5

k_2 = 0.5

t = np.arange(0, 52*3)

trend_1 = mu * t ** k_1

trend_2 = mu * t ** k_2

plt.figure(figsize=(18, 3))

plt.plot(t, trend_1, label='Trend1')

plt.legend()

plt.show()

plt.figure(figsize=(18, 3))

plt.plot(t, trend_2, label='Trend2', color="Orange")

plt.legend()

plt.show()

“k=1″で単調増加，”k>1″で指数増加し，”k<1″で対数増加します．トレンドはパラメータの値が変化することで，様々な非線形トレンド成分を表現します．

・季節性

季節性に関してはライブラリ内部に関数が定義されており，呼び出すだけで可視化することができます．関数は三角関数の合成和で定義されており，デフォルトの周期は”52″ですが（週次データを仮定），日次データを扱う場合には引数として”365″を渡してあげる必要があります．

# 季節項の作成
seasonality_1 = media_transforms.calculate_seasonality(number_periods=52*3, # 周期 * 年数 = データ長
                                                    degrees=3, # 山の個数
                                                    gamma_seasonality=1,
                                                    frequency=52 # 季節の周期 # 1周期の長さ
                                                    )
seasonality_2 = media_transforms.calculate_seasonality(number_periods=52*3, # 周期 * 年数 = データ長
                                                    degrees=2, # 山の個数
                                                    gamma_seasonality=2,
                                                    frequency=26 # 季節の周期 # 1周期の長さ
                                                    )

# Generate x-axis values
x_values = range(len(seasonality_1))
plt.figure(figsize=(18, 5))
plt.plot(x_values, seasonality_1, label='Seasonality1')
plt.plot(x_values, seasonality_2, label='Seasonality2')
plt.legend()
plt.show()

# 季節項の作成

seasonality_1 = media_transforms.calculate_seasonality(number_periods=52*3, # 周期 * 年数 = データ長

degrees=3, # 山の個数

gamma_seasonality=1,

frequency=52 # 季節の周期 # 1周期の長さ

)

seasonality_2 = media_transforms.calculate_seasonality(number_periods=52*3, # 周期 * 年数 = データ長

degrees=2, # 山の個数

gamma_seasonality=2,

frequency=26 # 季節の周期 # 1周期の長さ

)

# Generate x-axis values

x_values = range(len(seasonality_1))

plt.figure(figsize=(18, 5))

plt.plot(x_values, seasonality_1, label='Seasonality1')

plt.plot(x_values, seasonality_2, label='Seasonality2')

plt.legend()

plt.show()

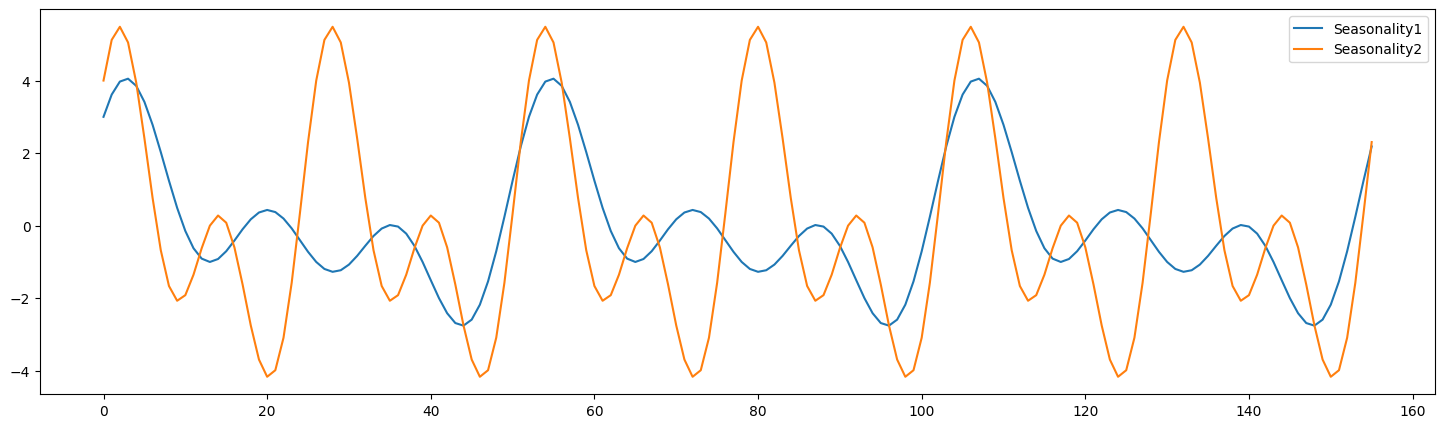
こちらも同様にパラメータの値が変化することで様々な季節性を表現することができます．

・メディア効果

続いて，各メディアの広告効果の非線形変換についてです．一般的に広告配信には，広告の効果が徐々に減りつつも残存する”ラグ効果”や，広告コストに対するリターンがどこかで頭打ちになる”飽和効果”があることが知られています．なので正しく広告効果をモデリングするためには，それらの効果もモデル内に組み込む必要があります．そこでLightweightMMMには”carry over”，”Ad stock”，”Hill Ad stock”の3種類のメディア効果の非線形変換関数が定義されています．これらの関数に各メディアの広告費等が入力され，広告のラグ効果や飽和効果をモデリングすることができます．実際にそれぞれの関数に”TV”の広告費を入力した時の非線形変換した結果が以下の図になります．

carry_over = media_transforms.carryover(media_data_train_scale[:, 0].reshape(-1, 1), ad_effect_retention_rate=0.5, peak_effect_delay=1, number_lags=13)
ad_stock = media_transforms.adstock(media_data_train_scale[:, 0].reshape(-1, 1),  lag_weight=0.9, normalise=True)
hill = media_transforms.hill(media_data_train_scale[:, 0].reshape(-1, 1), half_max_effective_concentration = 0.1, slope = 1)

x_values = range(len(carry_over))
plt.figure(figsize=(18, 5))
plt.plot(x_values, media_data_train_scale[:, 0], label='Original data', alpha=0.4)
plt.plot(x_values, carry_over, label='Carry over', alpha=0.8)
plt.plot(x_values, ad_stock, label='Ad Stock', alpha=0.8)
plt.plot(x_values, hill, label='Hill', alpha=0.8)
plt.legend()
plt.show()

carry_over = media_transforms.carryover(media_data_train_scale[:, 0].reshape(-1, 1), ad_effect_retention_rate=0.5, peak_effect_delay=1, number_lags=13)

ad_stock = media_transforms.adstock(media_data_train_scale[:, 0].reshape(-1, 1), lag_weight=0.9, normalise=True)

hill = media_transforms.hill(media_data_train_scale[:, 0].reshape(-1, 1), half_max_effective_concentration = 0.1, slope = 1)

x_values = range(len(carry_over))

plt.figure(figsize=(18, 5))

plt.plot(x_values, media_data_train_scale[:, 0], label='Original data', alpha=0.4)

plt.plot(x_values, carry_over, label='Carry over', alpha=0.8)

plt.plot(x_values, ad_stock, label='Ad Stock', alpha=0.8)

plt.plot(x_values, hill, label='Hill', alpha=0.8)

plt.legend()

plt.show()

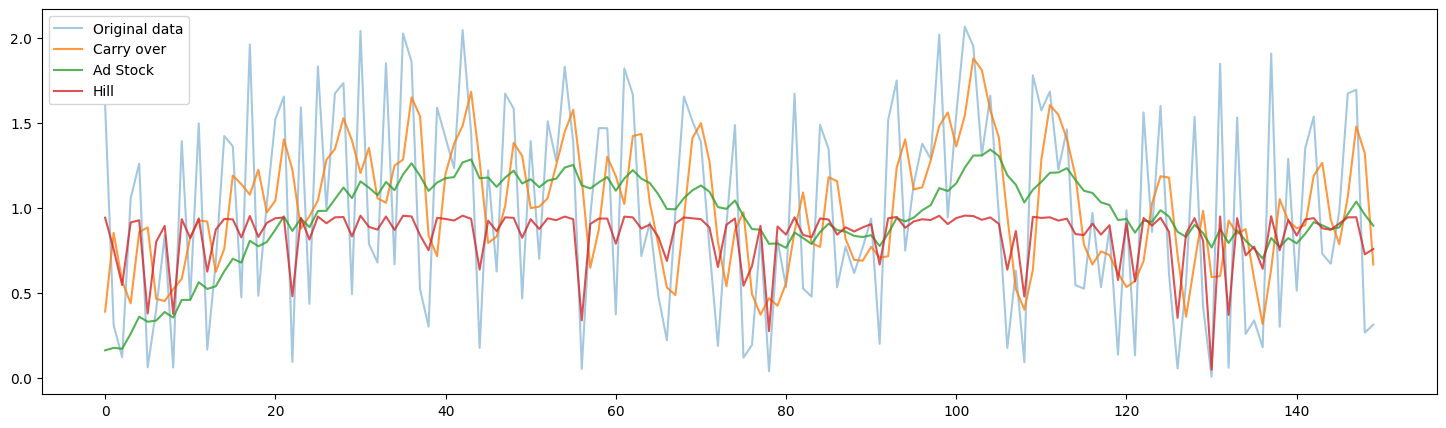
関数によって変換後の形状が異なることが確認できます．しかし上記の結果は一例に過ぎず，非線形変換後の形状は各関数のパラメータの値によって変化します．モデルはこれらのパラメータも学習過程において推定され，最適なラグ効果，及び飽和効果をモデリングします．

学習

それでは，実際にMCMCサンプリングを用いて学習していきます．今回はメディアの広告効果の非線形関数として”carry over”を使用します．

SEED = 123
mmm = lightweight_mmm.LightweightMMM(model_name="carryover") # carryover or adstock or hill_adstock
number_warmup=2000
number_samples=2000
number_chains = 3

# custom_priors = {"intercept": numpyro.distributions.HalfCauchy(scale=1)}
mmm.fit(
    media=media_data_train_scale,
    media_prior=costs_scale,
    target=target_train_scale,
    # extra_features=extra_features_train,
    number_warmup=number_warmup,
    number_samples=number_samples,
    seed=SEED,
    number_chains=number_chains,
    weekday_seasonality=False, #default
    seasonality_frequency=52 #default
    # weekday_seasonality=True,
    # seasonality_frequency=365
    # custom_priors=custom_priors
    )
mmm.print_summary()

SEED = 123

mmm = lightweight_mmm.LightweightMMM(model_name="carryover") # carryover or adstock or hill_adstock

number_warmup=2000

number_samples=2000

number_chains = 3

# custom_priors = {"intercept": numpyro.distributions.HalfCauchy(scale=1)}

mmm.fit(

media=media_data_train_scale,

media_prior=costs_scale,

target=target_train_scale,

# extra_features=extra_features_train,

number_warmup=number_warmup,

number_samples=number_samples,

seed=SEED,

number_chains=number_chains,

weekday_seasonality=False, #default

seasonality_frequency=52 #default

# weekday_seasonality=True,

# seasonality_frequency=365

# custom_priors=custom_priors

)

mmm.print_summary()

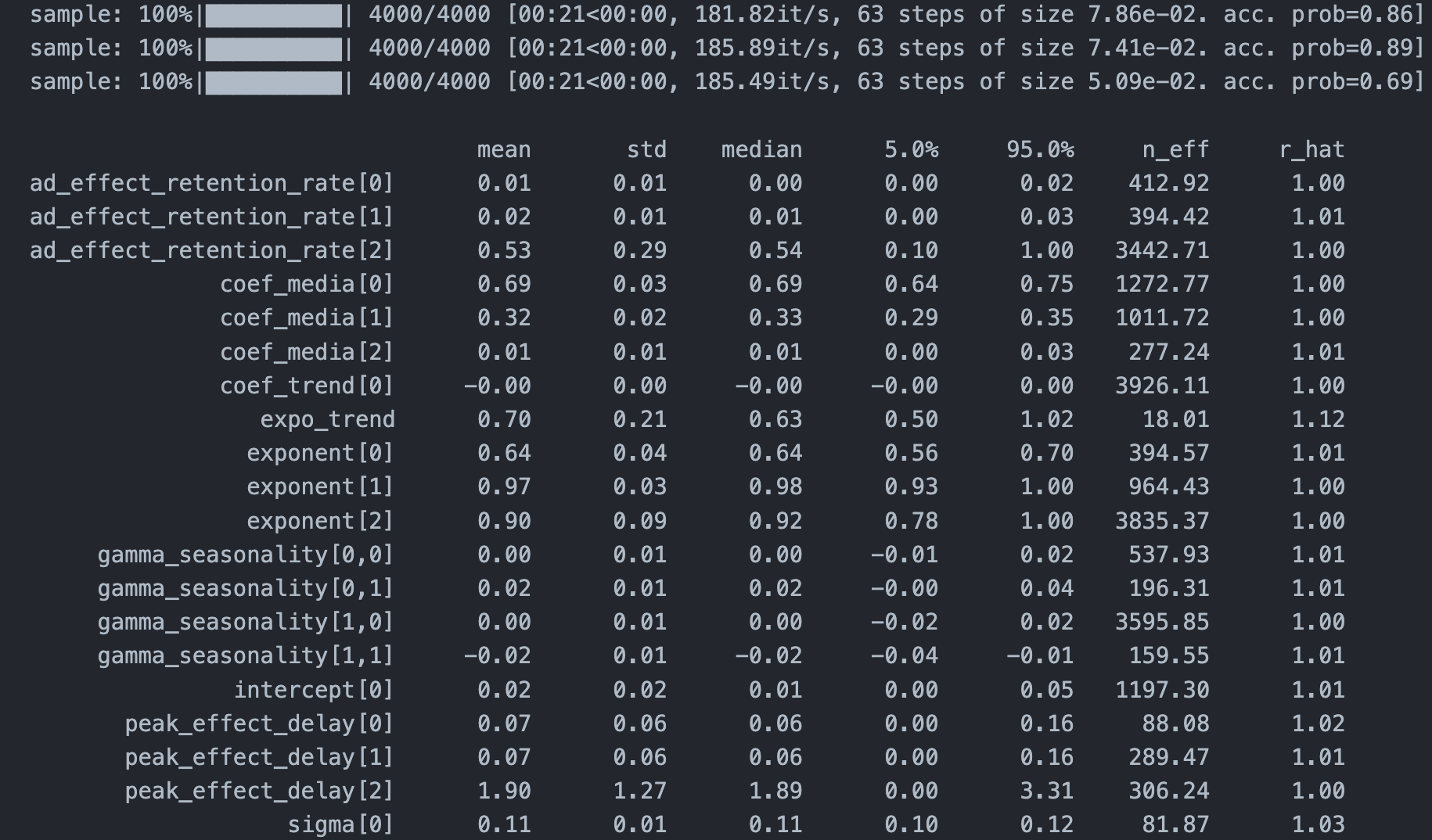
LightweightMMMはnumpyroを使ってMCMCサンプリングを行うので非常に高速に推定を行うことができるのが利点です．表示された結果の”r_hat”が収束判断指標となっており，これが1.1未満の時にサンプリングが収束しているとみなして良いそうです．結果より全てのパラメータにおいて収束していることが確認できます．またTV（coef_media[0]）の偏回帰係数が大きいことから，TV広告の売上貢献度が高いことが確認されました．

MCMCサンプル

MCMCサンプリングの過程を可視化してみます．これに関してはライブラリ内に良い感じの関数がなかったので自作しました．

for m in range(media_data_train_scale.shape[1]):
    samples_1, samples_2, samples_3 = jnp.split(mmm.trace["coef_media"][:, m], 3)
    samples = mmm.trace["coef_media"][:, m]
    fig, ax = plt.subplots(1, 2, figsize=(12, 2), gridspec_kw={'width_ratios': [3, 1]})
    ax[0].plot(samples_1, color="b", alpha=0.2)
    ax[0].plot(samples_2, color="b", alpha=0.2)
    ax[0].plot(samples_3, color="b", alpha=0.2)
    ax[1].hist(samples, orientation="horizontal", color="b", alpha=0.5, bins=100)
    fig.suptitle(media_names[m])

plt.figure(figsize=(12, 2))
samples_1, samples_2, samples_3 = jnp.split(mmm.trace["intercept"], 3)
samples = mmm.trace["intercept"].reshape(-1)
fig, ax = plt.subplots(1, 2, figsize=(12, 2), gridspec_kw={'width_ratios': [3, 1]})
ax[0].plot(samples_1, color="b", alpha=0.2)
ax[0].plot(samples_2, color="b", alpha=0.2)
ax[0].plot(samples_3, color="b", alpha=0.2)
ax[1].hist(samples, orientation="horizontal", color="b", alpha=0.5, bins=100)
fig.suptitle("intercept")

for m in range(media_data_train_scale.shape[1]):

samples_1, samples_2, samples_3 = jnp.split(mmm.trace["coef_media"][:, m], 3)

samples = mmm.trace["coef_media"][:, m]

fig, ax = plt.subplots(1, 2, figsize=(12, 2), gridspec_kw={'width_ratios': [3, 1]})

ax[0].plot(samples_1, color="b", alpha=0.2)

ax[0].plot(samples_2, color="b", alpha=0.2)

ax[0].plot(samples_3, color="b", alpha=0.2)

ax[1].hist(samples, orientation="horizontal", color="b", alpha=0.5, bins=100)

fig.suptitle(media_names[m])

plt.figure(figsize=(12, 2))

samples_1, samples_2, samples_3 = jnp.split(mmm.trace["intercept"], 3)

samples = mmm.trace["intercept"].reshape(-1)

fig, ax = plt.subplots(1, 2, figsize=(12, 2), gridspec_kw={'width_ratios': [3, 1]})

ax[0].plot(samples_1, color="b", alpha=0.2)

ax[0].plot(samples_2, color="b", alpha=0.2)

ax[0].plot(samples_3, color="b", alpha=0.2)

ax[1].hist(samples, orientation="horizontal", color="b", alpha=0.5, bins=100)

fig.suptitle("intercept")

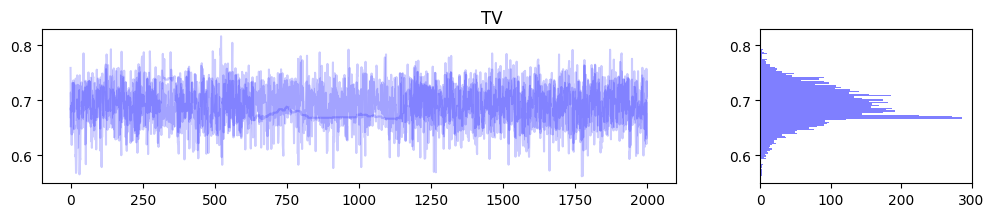
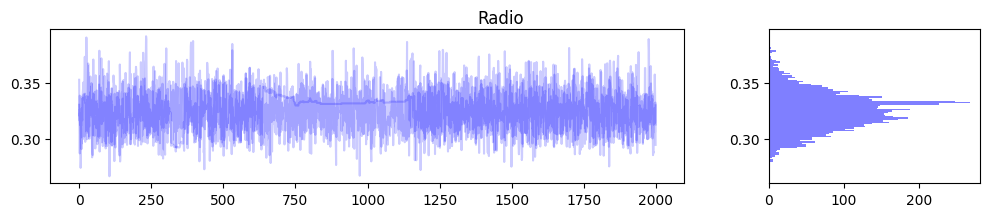
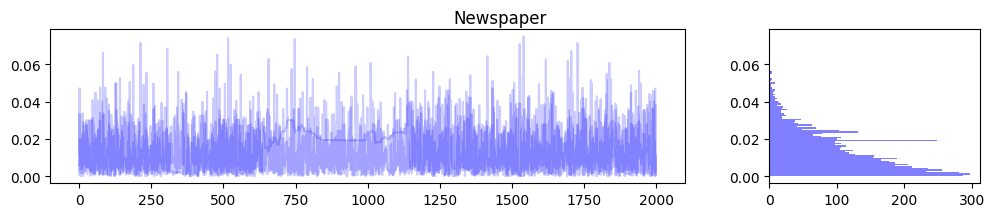
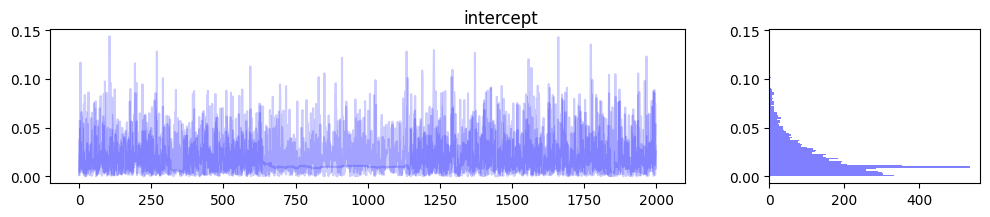
上記のようにパラメータに確率分布を仮定しているのがベイズ推定の嬉しいポイントですね．これにより推定の不確実性が可視化されるため，ビジネス的な意思決定をする際の1つの良い判断材料になることが期待できます．また変数間に多重共線性がある場合，推定された偏回帰係数の値が不安定になる傾向があるのですが，このようにパラメータの分布を確認できることで，その影響度合いを可視化できるのもベイズ推定のメリットの1つです．

学習精度

学習データへのフィッティング度合いも確認してみます．

plot.plot_model_fit(mmm, target_scaler=target_scaler)

1	plot.plot_model_fit(mmm, target_scaler=target_scaler)

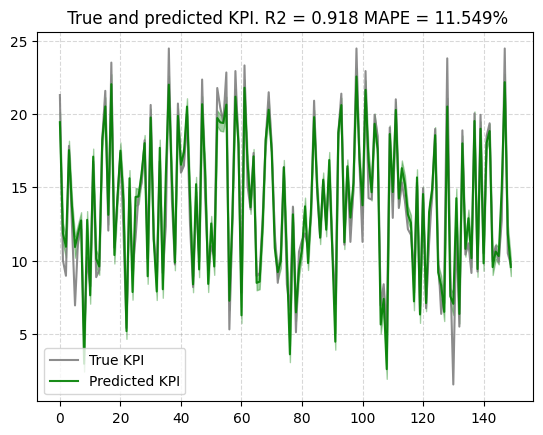
精度とベイズ信用区間から，学習データに対し上手く学習できていることが確認できます．

予測

テスト精度

続いてテストデータセットに対する予測精度を見ていきます．

target_predict = mmm.predict(
    media=media_data_test_scale,
    target_scaler=target_scaler
)

plot.plot_out_of_sample_model_fit(out_of_sample_predictions=target_predict, out_of_sample_target=target_test)

target_predict = mmm.predict(

media=media_data_test_scale,

target_scaler=target_scaler

)

plot.plot_out_of_sample_model_fit(out_of_sample_predictions=target_predict, out_of_sample_target=target_test)

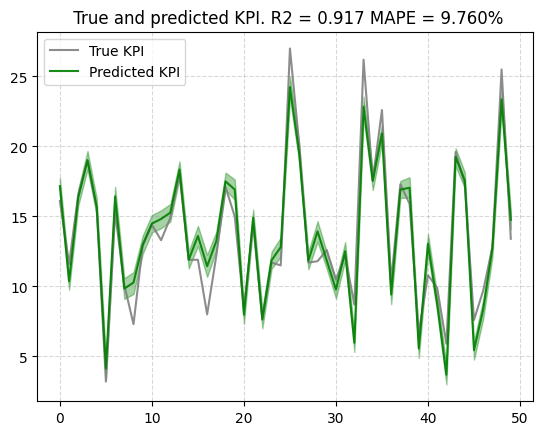
学習されたモデルはテストデータに対しても，精度良く予測できており，ベイズ予測区間も安定しています．

解釈

メディア貢献度

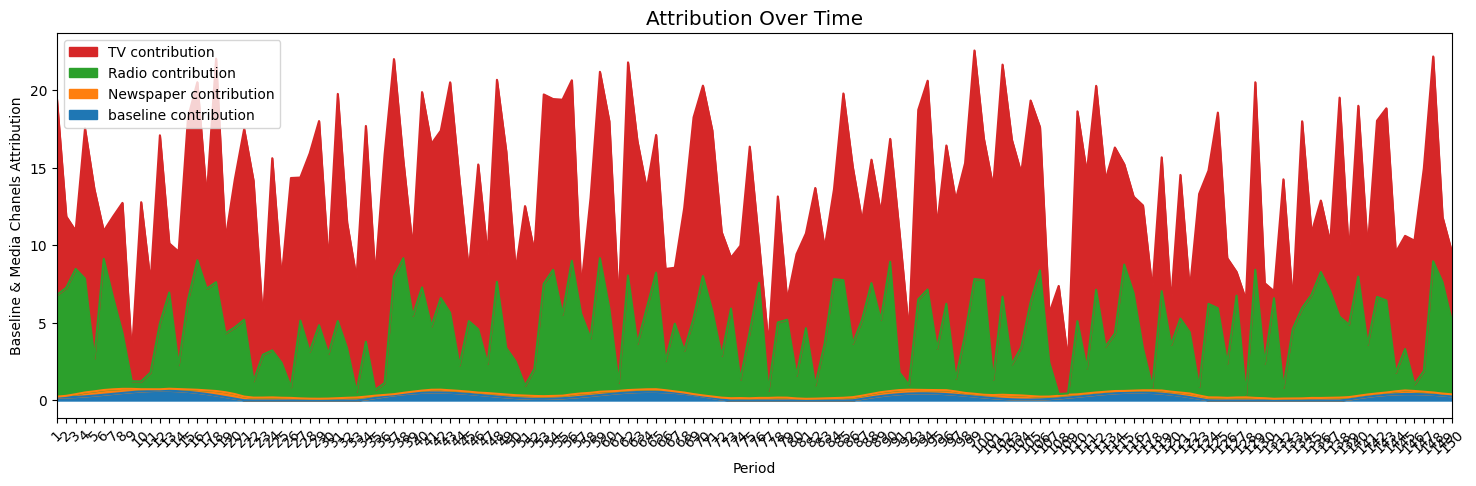
LightweightMMMはSalesに対する各メディアの貢献度を時系列データとして可視化することもできます．

plot.plot_media_baseline_contribution_area_plot(mmm, target_scaler=target_scaler, fig_size=(18, 5), channel_names=media_names)

1	plot.plot_media_baseline_contribution_area_plot(mmm, target_scaler=target_scaler, fig_size=(18, 5), channel_names=media_names)

これを見ると，売上に対してTV広告の貢献度が高いことが確認できます．

広告投資効果（ROAS）

各メディアのROAS は以下になります．ROASは以下の式によって算出され，この値が大きいほど費用対効果が高いと解釈することができます．

ROAS = (広告からの売上) / (広告コスト) × 100

plot.plot_bars_media_metrics(metric=roi_hat, channel_names=media_names)

1	plot.plot_bars_media_metrics(metric=roi_hat, channel_names=media_names)

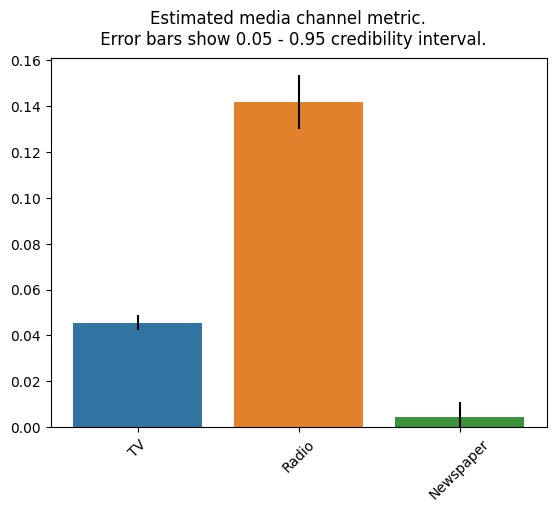
結果を見てみると，意外にもラジオ広告の費用対効果が大きい様子です．

予算最適化

LightweightMMMは予算配分の最適化も行うことができます．今回は学習データに含まれる予算で，テストデータの期間に対して最適な予算配分を算出します．

prices = jnp.ones(mmm.n_media_channels)
n_time_periods = media_data_test.shape[0]
budget = jnp.sum(media_data_train.mean(axis=0)) * n_time_periods

solution, kpi_without_optim, previous_budget_allocation = optimize_media.find_optimal_budgets(
    n_time_periods = n_time_periods,
    prices = prices,
    budget = budget,
    media_mix_model = mmm,
    media_scaler = media_scaler,
    target_scaler = target_scaler,
    seed = SEED
)

optimal_budget_allocation = prices * solution.x
print(f"Budget: {budget},\nSum of Optimal Budget Allocation: {optimal_budget_allocation.sum()}")
print(f"Optimal Budget Allocation: {optimal_budget_allocation}")

plot.plot_pre_post_budget_allocation_comparison(media_mix_model=mmm,
                                                kpi_with_optim=solution['fun'],
                                                kpi_without_optim=kpi_without_optim,
                                                optimal_buget_allocation=optimal_budget_allocation,
                                                previous_budget_allocation=previous_budget_allocation,
                                                figure_size=(10,10))

prices = jnp.ones(mmm.n_media_channels)

n_time_periods = media_data_test.shape[0]

budget = jnp.sum(media_data_train.mean(axis=0)) * n_time_periods

solution, kpi_without_optim, previous_budget_allocation = optimize_media.find_optimal_budgets(

n_time_periods = n_time_periods,

prices = prices,

budget = budget,

media_mix_model = mmm,

media_scaler = media_scaler,

target_scaler = target_scaler,

seed = SEED

)

optimal_budget_allocation = prices * solution.x

print(f"Budget: {budget},\nSum of Optimal Budget Allocation: {optimal_budget_allocation.sum()}")

print(f"Optimal Budget Allocation: {optimal_budget_allocation}")

plot.plot_pre_post_budget_allocation_comparison(media_mix_model=mmm,

kpi_with_optim=solution['fun'],

kpi_without_optim=kpi_without_optim,

optimal_buget_allocation=optimal_budget_allocation,

previous_budget_allocation=previous_budget_allocation,

figure_size=(10,10))

Optimization terminated successfully    (Exit mode 0)
            Current function value: -743.7722355980677
            Iterations: 14
            Function evaluations: 98
            Gradient evaluations: 14
Budget: 10014.2333984375,
Sum of Optimal Budget Allocation: 10014.234375
Optimal Budget Allocation: [7832.4336 1159.56   1022.24  ]

Optimization terminated successfully (Exit mode 0)

Current function value: -743.7722355980677

Iterations: 14

Function evaluations: 98

Gradient evaluations: 14

Budget: 10014.2333984375,

Sum of Optimal Budget Allocation: 10014.234375

Optimal Budget Allocation: [7832.4336 1159.56 1022.24 ]

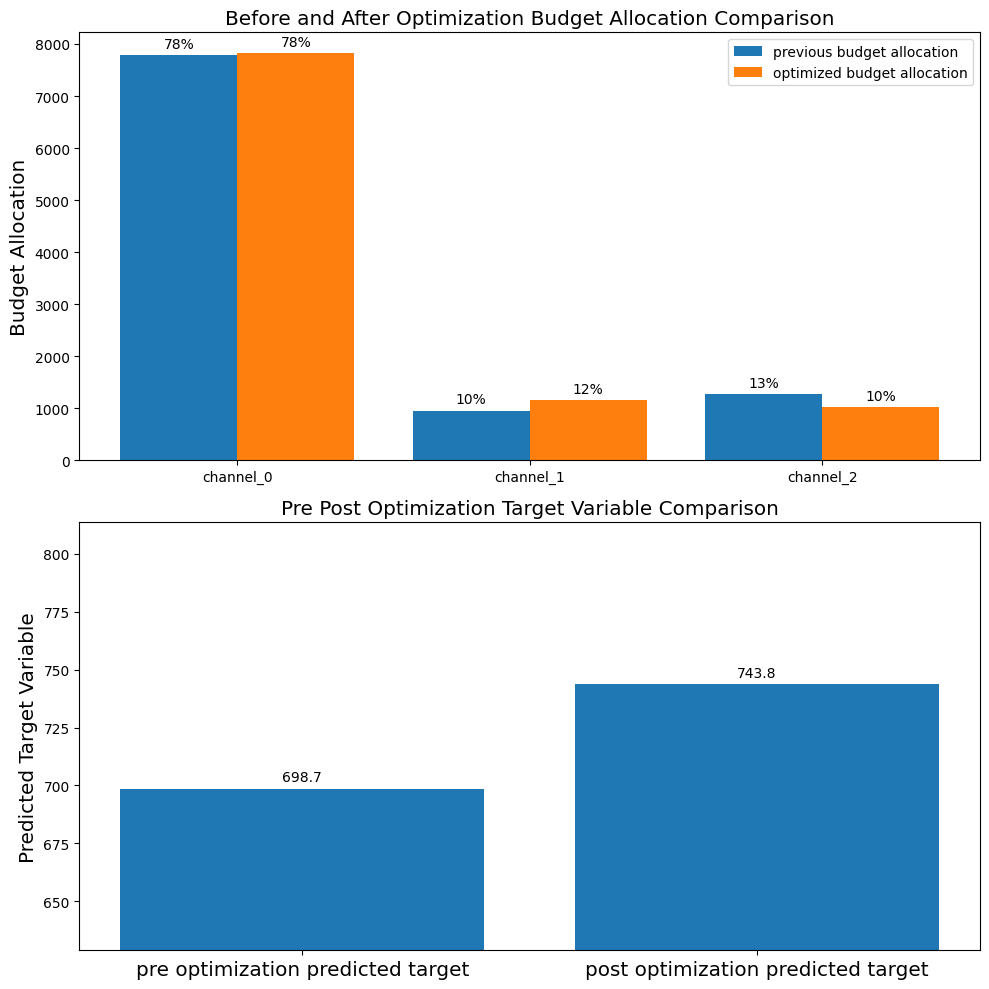
結果を見てみると費用対効果の高いラジオ広告の予算配分がやや増加していることがわかります．また今回は従来の投資配分と最適化された投資配分間に大きな差はありませんが，ハイパーパラメータを変えることで従来との乖離度合いを調整することができるみたいです．

モデルの保存

以下のコードで推定したモデルを保存することができます．これによりいつでも学習済みのモデルを呼び出すことができます．

file_path = "media_mix_model.pkl"
utils.save_model(media_mix_model=mmm, file_path=file_path)

loaded_mmm = utils.load_model(file_path="media_mix_model.pkl")
print(f'loaded_mmm coef_media shape: {loaded_mmm.trace["coef_media"].shape}')

file_path = "media_mix_model.pkl"

utils.save_model(media_mix_model=mmm, file_path=file_path)

loaded_mmm = utils.load_model(file_path="media_mix_model.pkl")

print(f'loaded_mmm coef_media shape: {loaded_mmm.trace["coef_media"].shape}')

loaded_mmm coef_media shape: (6000, 3)

1	loaded_mmm coef_media shape: (6000, 3)

所感

LightweightMMM主要機能を一通り実装してみて，個人的にはMMMの全体感が掴めてとても勉強になりました．ただ実務で扱うようなデータは今回扱ったような綺麗なデータであるとは限らないですし，多重共線性や交絡など考慮しなければならないことが多くあるので，その辺も考慮した分析ができるようになりたいです．またMMMでは時系列データを扱うということで，状態空間モデルに拡張したり，他の時系列解析のライブラリと組み合わせたりと，より柔軟性の高いモデルでMMMを行ってみたいと思いました．

引用論文

Y. Jin et al. “Bayesian Methods for Media Mix Modeling with Carryover and Shape Effects”. 2017

告知

明日は天河さんによる「inputタグ, textarea内のキャレット座標（カーソルの位置）を取得する」です！引き続きGMOアドマーケティング Advent Calendar 2023 をお楽しみください！

■エンジニア採用ページはこちら！
https://recruit.gmo-ap.jp/

■GMOアドパートナーズ公式noteはこちら！
https://note.gmo-ap.jp/

kantayama

はじめに

マーケティング・ミックス・モデリング（MMM）とは

概要

なぜ，今MMMが必要？

LightweightMMM

実装

ライブラリのインポート

データの確認

時系列プロット

共分散混合行列

VIF

前処理

モデル

・トレンド

・季節性

・メディア効果

学習

MCMCサンプル

学習精度

予測

テスト精度

解釈

メディア貢献度

広告投資効果（ROAS）

予算最適化

モデルの保存

所感

引用論文

告知

おすすめ

Railsのタグ機能でN+1問題解消

Professional Scrum Master ⅠとⅡに合格しました

background-imageを活用して、アップする画像を1個で済ませたい