GMOアドマーケティングのT.Nです。
第9回の勉強会を開催しました。
今回は、回帰分析について学んだので、Pythonを使った回帰分析について書きます。

Pythonを使った回帰分析

今回は、陸上短距離の100mに関する分析を行いました。

2004年以降の世界選手権、オリンピックの男子100mの優勝タイムが、
どのような要素と関連しているのかを分析しました。

今回は、GoogleのColaboratoryで分析を行いました。
Colaboratoryは、クラウドで実行できるJupyter Notebookのようなものです。
スプレッドシートなどのような手軽さで、簡単にPythonを実行できるので便利です。
Colaboratory

分析手順

1. CSVファイルのアップロード

Colaboratoryに分析に使用するデータのCSVファイルをアップロードします。
今回は、ローカルのファイルをアップロードして使用しました。
ソースコードは以下のページを参考にしました。

https://colab.research.google.com/notebooks/io.ipynb

上記の処理を実行すると、以下のように「ファイル選択」というボタンが表示されるので、
ボタンを押してアップロードします。

2. pandasでデータを処理する

アップロードしたファイルを、pandasを使用して読み込みます。

上記の処理により、以下のような表が出力されます。

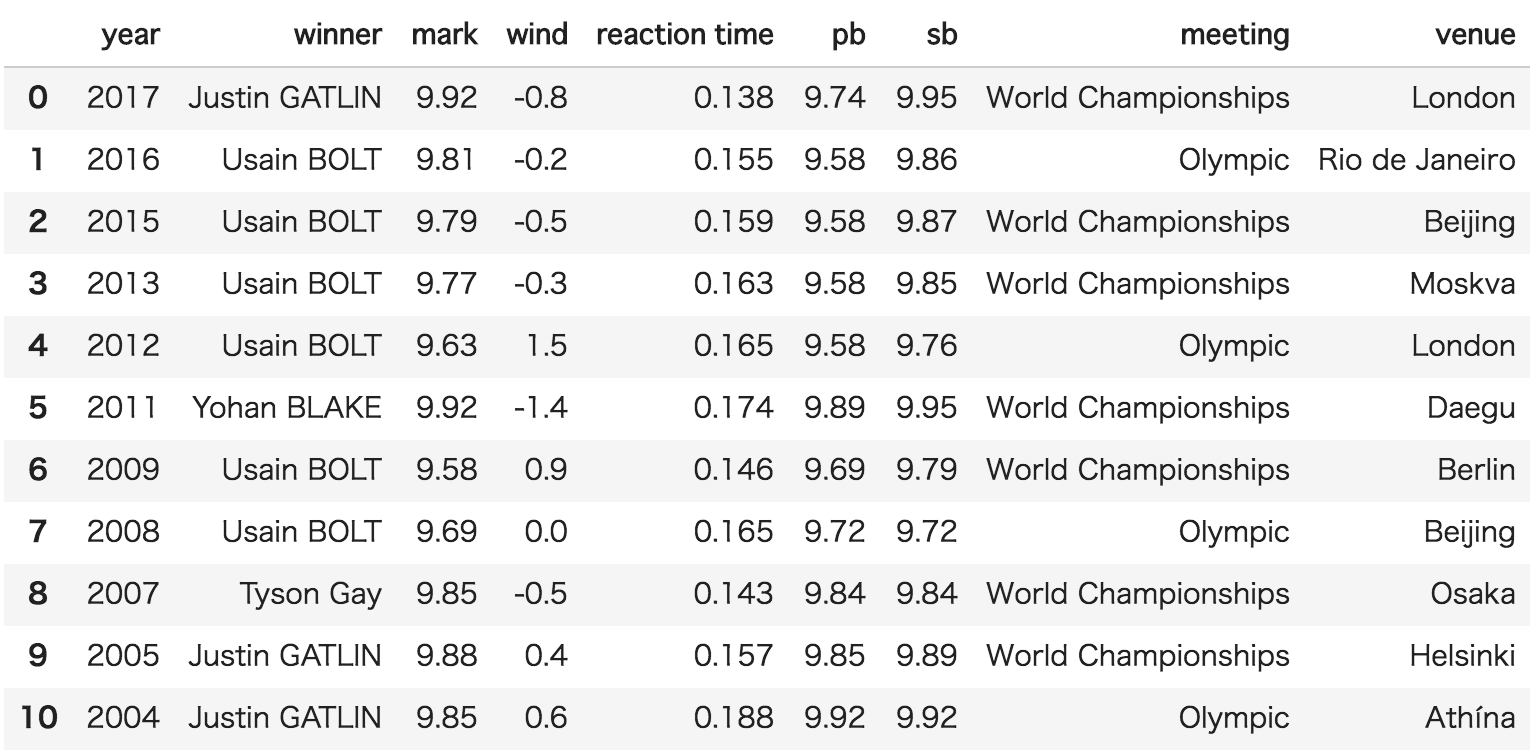
世界レベルの大会ということもあり、2004年以降の優勝タイムは全て9秒台です。
このようにして見ると、
2008年から2016年までのウサイン・ボルト選手の強さが圧倒的であることが分かります。
2011年の大邱大会では、フライングで失格になってしまいましたが、
その時に優勝したヨハン・ブレーク選手は、
後に100m、200mでそれぞれ世界歴代2位の記録を出す活躍を見せています。

2007年の大阪大会は会場で観ていましたが、
タイソン・ゲイ選手とアサファ・パウエル選手のどちらが勝つかわからない状況で、
最後にタイソン・ゲイ選手が抜け出たシーンが印象に残っています。
ちなみに、ウサイン・ボルト選手は大阪大会では200mで2位でした。

pandasでデータを整えただけで、過去のレースの記憶が蘇ってきますね。
次の手順で、実際に分析を行いたいと思います。

3. 回帰分析を実行する

目的変数、説明変数を以下のように設定して分析を行いました。

目的変数

mark

優勝タイム

説明変数

wind	風速
reaction time	スタートの反応速度
pb	優勝した選手の大会当日の自己ベスト
sb	優勝した選手の大会当日のシーズンベスト

回帰分析は、以下のソースコードで実行できます。
dfという変数には、前の手順でpandasで読み込んだデータが入っています。

今回は、以下の2通りの説明変数で分析を行いました。

モデル1

mark(優勝タイム) ~ wind(風速) + reaction time(反応速度) + pb(自己ベスト) + sb(シーズンベスト)

モデル2

mark(優勝タイム) ~ wind(風速) + pb(自己ベスト) + sb(シーズンベスト)

4. 結果の分析

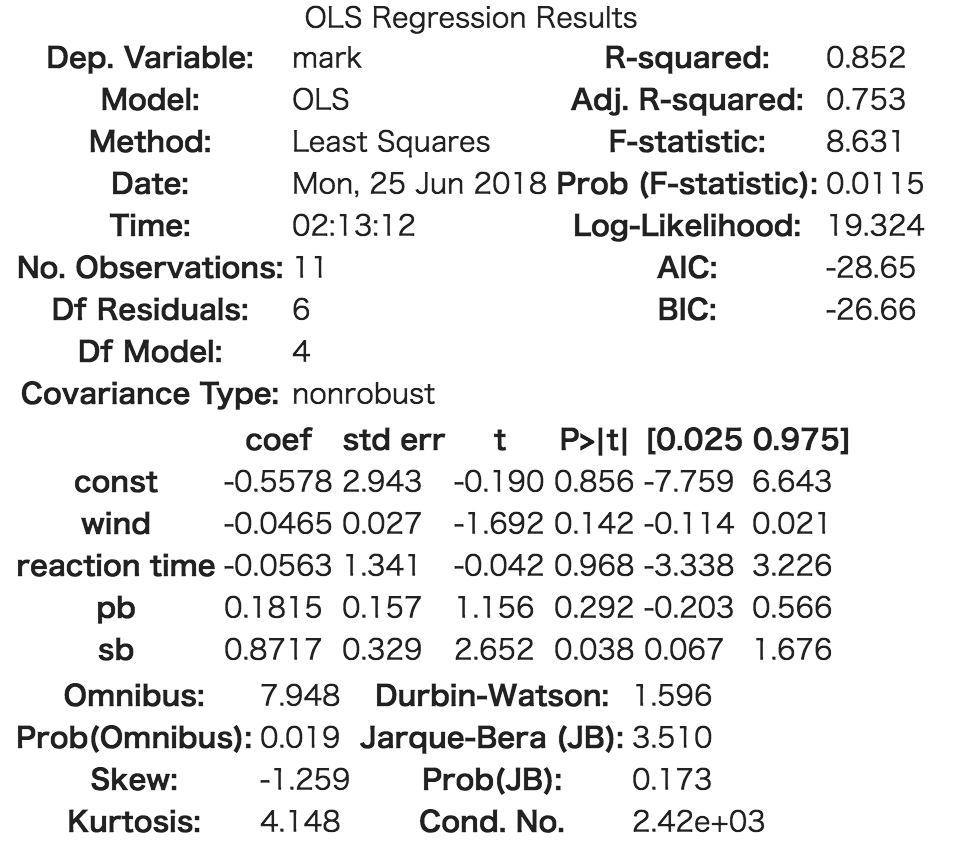
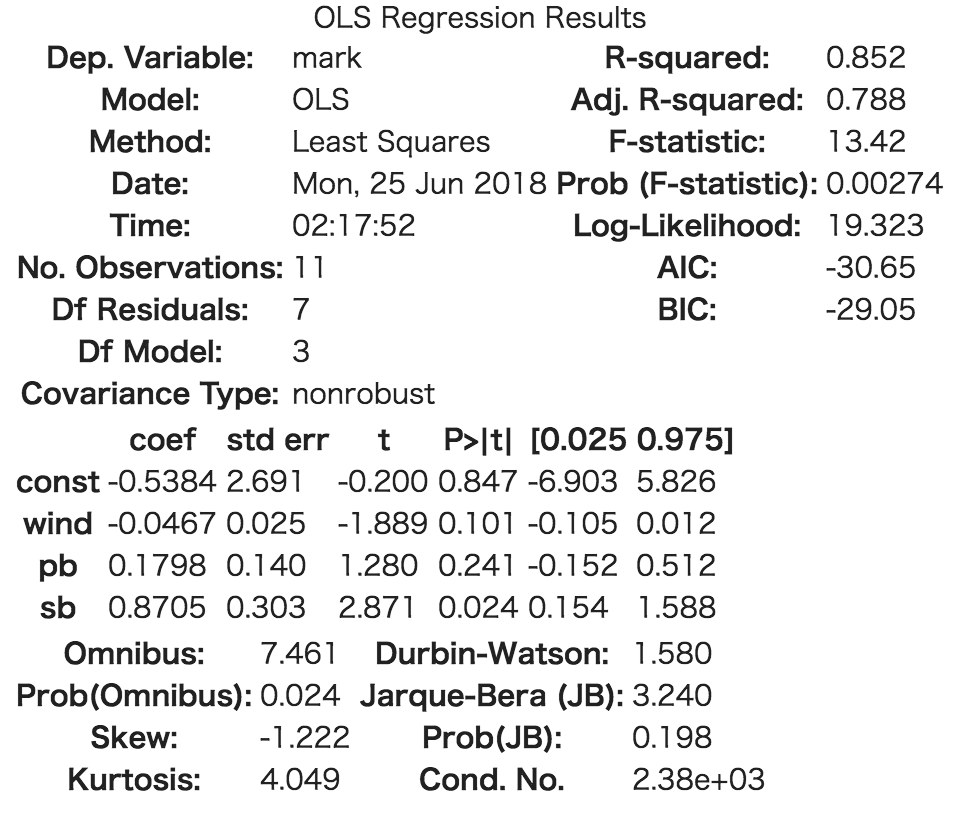
手順3のソースコードを実行すると、以下のような表が出力されます。

モデル1の結果

モデル2の結果

まずは右上の部分に注目します。

モデル1

モデル2

用語の説明

R-squared	決定係数
Adj. R-squared	自由度調整済決定係数

決定係数は、全変動のうち、回帰値による変動の割合を表すもので、
1に近くなるほど、回帰式に説明力があると言えます。
ただ、説明変数が増加すると、決定係数も増加するという性質があるため、
分析の際には、自由度調整済決定係数を使用します。

今回は、
モデル1: 0.753
モデル2: 0.788
という値になっていて、どちらも悪くはないと言えそうです。
2の方が、少しだけモデルの当てはまりが良さそうです。

次に、各係数の推定値が有意であるかを判断します。
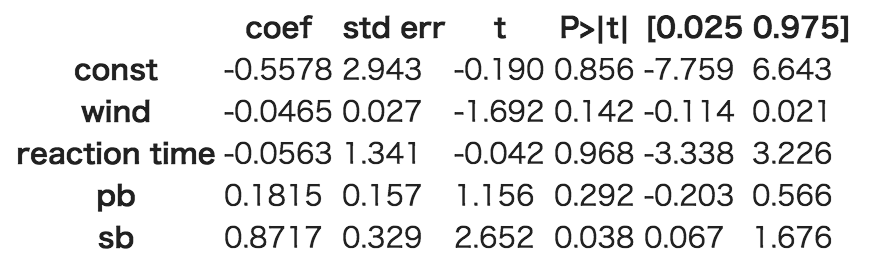
係数に関する結果は、中段に出力されます。

モデル1

モデル2

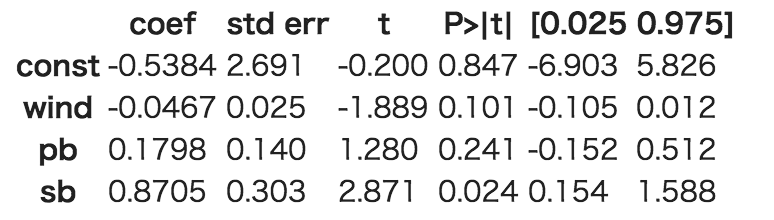
用語の説明

coef	回帰係数の推定値
std err	標準誤差
t	t検定の検定統計量
P>|t|	t検定のP値
[0.025 0.975]	回帰係数の信頼率95%の信頼区間の下限と上限

この場合のt検定は、「回帰係数が0である」という帰無仮説を設定した検定です。
回帰係数が0であるというのは、説明変数が目的変数に影響しないということです。
この帰無仮説を棄却できれば、説明変数には意味があると考えることができます。
有意水準5%の場合は、P値が0.05より小さければ、帰無仮説を棄却できます。

今回は、有意水準5%で棄却できるのは、sbのみで、
それ以外は棄却できないという結果になりました。
モデルの説明変数は、sbのみでも、優勝タイムをある程度説明できると言えそうです。
計算量を減らしたい場合などは、説明変数から外しても良さそうです。

また、F検定の結果にも注目します。

モデル1

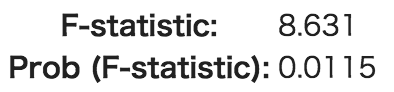
モデル2

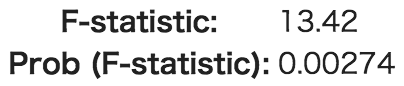
用語の説明

F-statistic	F検定の検定統計量
Prob (F-statistic)	F検定のP値

この場合のF検定は、「全ての回帰係数が0である」という帰無仮説を設定した検定です。
この帰無仮説を棄却できれば、少なくとも一つは回帰係数が0ではないと考えることができます。
今回は、どちらのモデルでも、有意水準5%で棄却できるので、問題はなさそうです。

ちなみに、風の係数、スタート時の反応速度の係数がマイナスになっているのは、
追い風が強くなるほど、また、反応速度が速くなるほど、
タイムが速くなる(回帰値が小さくなる)と考えられるためです。

風の係数、反応速度の係数が小さいのは、
追い風が強い、または、スタートの反応が良いからといって、
全ての選手がウサイン・ボルト選手のように走れるわけではないので、
直感的にも正しそうです。

自己ベストは、シーズンベストと比較すると、係数が小さいですが、
シーズンベストが悪くても、大会当日までに調子を戻して、
持っている力を発揮するということもあるので、
風や反応速度よりも影響が大きいのかもしれません。

今回は、自由度調整済決定係数が一番高い、モデル2を採用することにしました。

モデル2

ところで、先日山口県で日本選手権が開催され、
100mでは、山縣選手が勝負強さを見せ、10秒05で優勝しました。
今回作成したモデルを、日本選手権の結果に当てはめてみようと思います。

説明変数

wind (風速)	0.6
pb (大会当日の自己ベスト)	10.00
sb (大会当日のシーズンベスト)	10.12

以下のように計算しました。

結果は、
10.041
となり、優勝タイムの10秒05に近い値になりました。

今回の分析では、
優勝した選手の大会の年の調子が、そのまま大会の記録にも影響しやすいということが分かりました。
世界選手権、オリンピックを見る際には、シーズンベストに注目すると良いのかもしれません。

5. まとめ

今回は、Pythonを使った回帰分析の方法を紹介しました。
Pythonで回帰分析を行うのは、簡単にできますが、
重要なのは、結果を見てどう判断するかだと思います。
いろいろなデータを分析することで、データの見方を身につけていくのが良いと思いました。