この記事は GMOアドマーケティング Advent Calendar 2020 4日目の記事です。
はじめ
こんにちは。 GMOアドマーケティングのS.Sです。
時系列データの中には、株価のreturnデータのように変動の大きさが時間とともに変動するようなものがあります。
今回の記事ではARCHモデルを使って、時系列データの変動の大きさを見積もってみたいと思います。
データの準備
大きく株価が変動するようなイベントというと、2008年のサブプライム危機があったので、その時期の変動の大きさの変化をある程度モデルでも捉えることができればよさそうということにします。
サブプライムの直前の時期のアップルの株価データがmatplotlibのサンプルに含まれているので、以下からダウンロードします。
株価のlogarithmic differenceをとるのは大雑把に日次の変化率を計算するためです。
https://github.com/matplotlib/sample_data/blob/master/aapl.csv
|
1 |
! pip install numpy pandas arch matplotlib scipy |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np from arch import arch_model import matplotlib.pyplot as plt from scipy.stats import binom_test import pandas as pd df = pd.read_csv("aapl.csv") df["Date"] = pd.to_datetime(df["Date"]) df = df.sort_values(["Date"]) df["orig"] = df["Close"] df["pct_diff"] = df["orig"].apply(np.log).diff() df = df.dropna() df.head() |
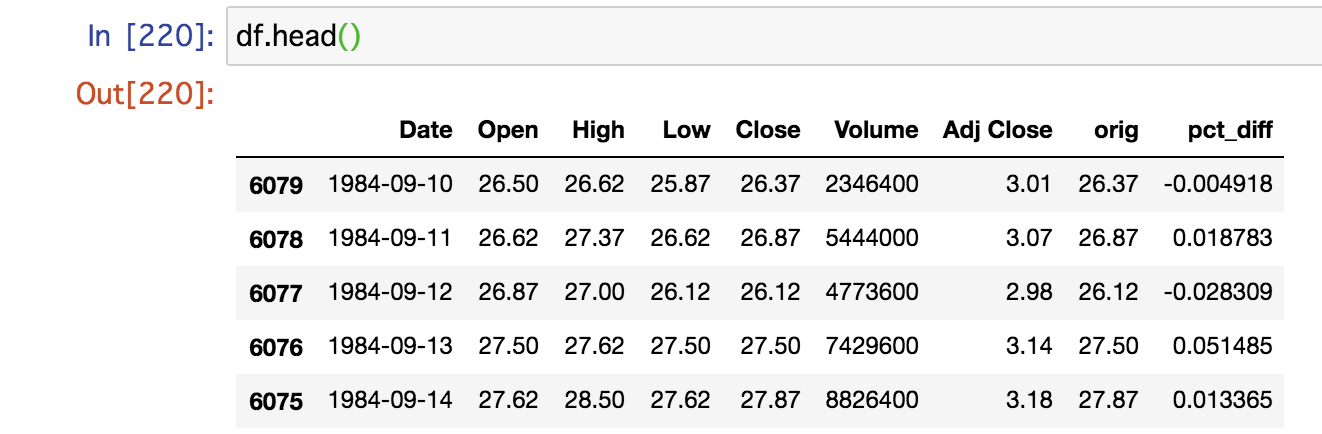
日次リターンの分布
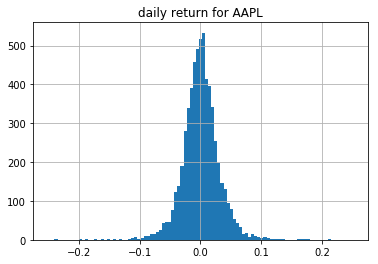
株を保有していると株価の上下に応じて利益や損失が発生します。
以下では株価の増加率をplotしてみました。
この記事では大きな損失が発生するタイミングを大雑把に見積もれればよいものとします。(図の左の裾のほうにくるタイミング)
これは株価が下がると予測するというよりは大きく株価が動くタイミングがおおまかにわかればよいという意味です。
動いた結果、株価が下がっていた場合は損失となります。
|
1 |
df["pct_diff"].hist(bins=np.linspace(-0.25, 0.25, 100)) |
モデルのfitting
モデルのfitに使う期間は2000/01/01~2008/05/31、テストデータの期間は2008/06/01~2008/10/14(データの終了日)とします。
|
1 2 |
begin_date = pd.to_datetime("2000-01-01") test_date = pd.to_datetime("2008-06-01") |
該当する期間のデータを取得して、ARCHモデルをfitします。
|
1 2 3 4 |
ser = df.loc[lambda x: (x["Date"] >= begin_date)].set_index(["Date"])["pct_diff"] * 100 am = arch_model(ser, p=1, o=0, q=1, dist='t') res = am.fit(update_freq=5, last_obs=(test_date - pd.offsets.Day(1)).strftime("%Y-%m-%d")) print(res.summary()) |
今回はGARCH(1,1)モデルを使います。
![]()
1step前に大きな変動があった場合(第二項)やその少し前に大きな変動があった場合(第三項)は、現時点での変動の大きさの見積もりに反映されます。
裾の予測の評価
今回は変動の大きさが大きくなり、大きなlossが出る可能性があるかどうかを知りたいので、returnの分布の下の裾の1%, 5%の値がどのくらいになるかを予測します。
この値はValue at Riskと呼ばれます。
株価のreturnデータの分析だと、lossを中心に考えることが多いので、以降ではreturnの符号を反転させて扱うものとします。
|
1 2 3 4 5 6 |
forecasts = res.forecast(start=test_date.strftime("%Y-%m-%d")) cond_mean = forecasts.mean[test_date.strftime("%Y-%m-%d"):] cond_var = forecasts.variance[test_date.strftime("%Y-%m-%d"):] q = am.distribution.ppf([0.01, 0.05], res.params[-1:]) print(q) value_at_risk = -cond_mean.values - np.sqrt(cond_var).values * q[None, :] |
得られた裾の1%, 5%の位置の見積もりが、どの程度正確かをここから調べて行きたいと思います。
|
1 2 3 4 |
df_result = ser.loc[lambda x: x.index >= pd.to_datetime("2008-06-01")].rename("orig_pct")\ .to_frame()\ .assign(orig_pct=lambda x: -x["orig_pct"], q_001=value_at_risk[:, 0], q_005=value_at_risk[:, 1]) dfi = df_result.reset_index() |
はじめに裾の予測と実際の観測値をplotしてみます。
|
1 2 3 4 5 6 7 |
plt.figure(figsize=(11, 6)) plt.scatter(dfi["Date"], dfi["orig_pct"]) plt.plot(dfi["Date"], dfi["q_001"], label="0.01") plt.plot(dfi["Date"], dfi["q_005"], label="0.05") plt.title("pct change and Value at Risk") plt.legend() plt.ylim(-1, 21) |
下図の青, 赤線がそれぞれ分布の1%, 5%の位置となります。
ぱっとみた感じでは、サブプライムの問題が起きた時期にかけて裾が動き、より大きなlossが起きるという見積もりになっていてよさそうです。
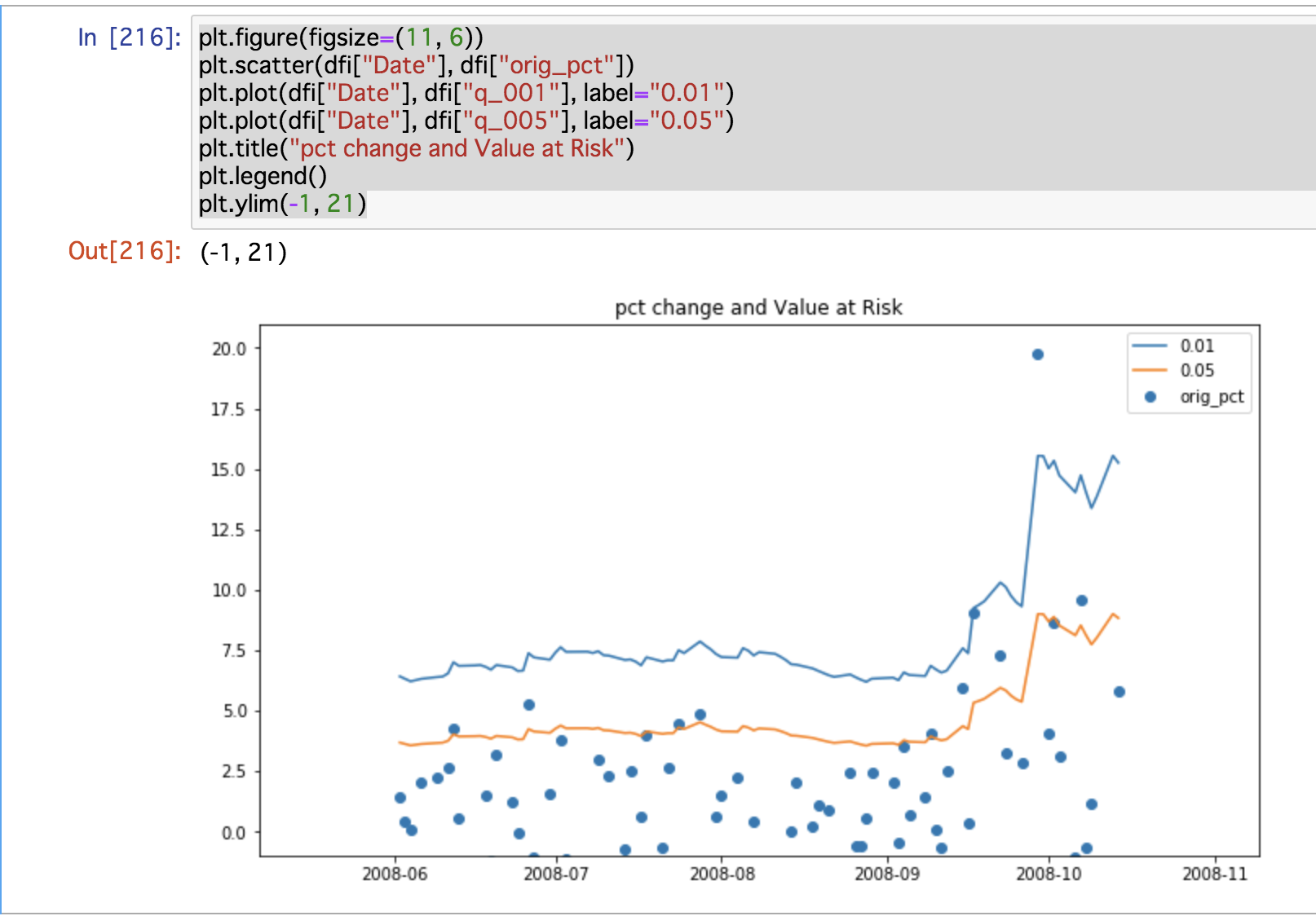
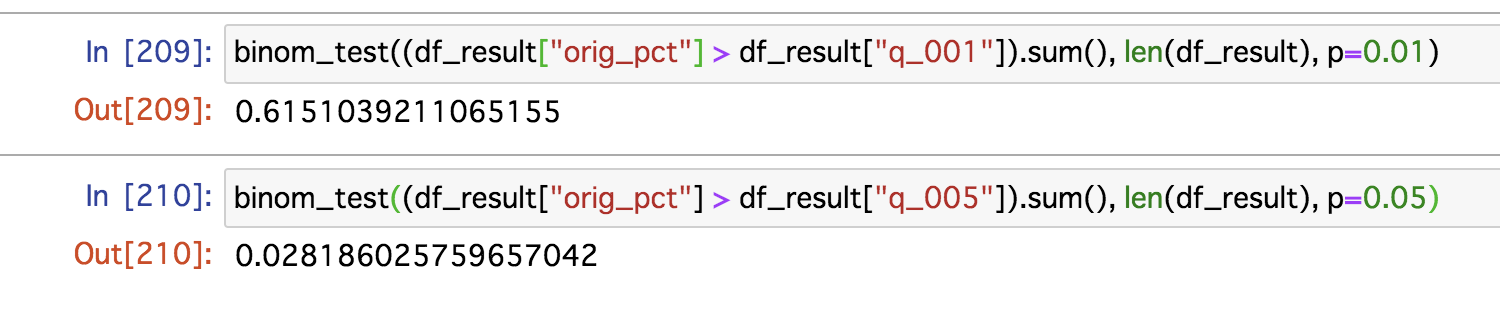
lossの分布の裾の1%, 5%の見積もりを出しているので、それより大きいlossが起きる確率はだいたい1%, 5%くらいになっていてほしいですが、大きくずれていないかどうかをbinomial testで確認してみます。
binomial testでは、出力が2値の試行を行なった結果と与えた確率がずれていないかをチェックします。
以下でp-valueを出してみましたが、99%の水準でみると裾の1%, 5%の見積もりに大きなズレはないといえそうです。(0.61 > 0.01, 0.02 > 0.01)
|
1 2 |
binom_test((df_result["orig_pct"] > df_result["q_001"]).sum(), len(df_result), p=0.01) binom_test((df_result["orig_pct"] > df_result["q_005"]).sum(), len(df_result), p=0.05) |
まとめ
今回の記事では、サブプライム危機直前のAppleの株価データを使って、ARCHモデルによる時系列データの変動の大きさの見積もりを試してみました。
今回の方法でも大雑把な見積もりくらいにはなるかと思います。
いかがでしたでしょうか。
明日は、tfactoryさんによる「BigQueryのユーザー定義関数(UDF)を使ってみる」です。
引き続き、GMOアドマーケティング Advent Calendar 2020 をお楽しみください!
■エンジニア採用ページ ~福利厚生や各種制度のご案内はこちら~
https://www.gmo-ap.jp/engineer/
■noteページ ~ブログや採用、イベント情報を公開中!~
https://note.gmo-ap.jp/




