反復の分解と再構築

はじめまして。 2021年8月にGMO NIKKOへ中途入社したshunkiです。

企業のテックブログに記事を投稿するのは前職を含めて初めてです。転職という挑戦をしたばかりなので、勢いに任せて投稿にも挑戦しました。これからも機会があれば挑戦させていただければと思っています。

また、今のところエンジニアパートナーの方々と関わる機会があまりありません。従事している業務が離れているのと、入社したばかりだからです。ただ、これからお世話になる事も多々あると思っています。その際に、この記事を話の種に交流できたらな、優しくしてもらえたらな、といった下心もあって投稿しています（笑）。

この記事の目標
判別共用体
状態機械
隠遁者の具体例：階乗
生産者の具体例：カウントダウン
消費者の具体例：総乗
生産消費者の具体例：ひとつ飛ばし
生産消費者の再構築の具体例：ひとつ飛ばし
終わりに
付録：状態機械の接続

この記事の目標

この記事の目標は次の謎めいた図式の主張を説明することです。そして、図式の具体例をJavaScriptのコードで示すことです。ただし、厳密な話は目標に入っていません。例えば数学的な定義を与えて証明することはしません。

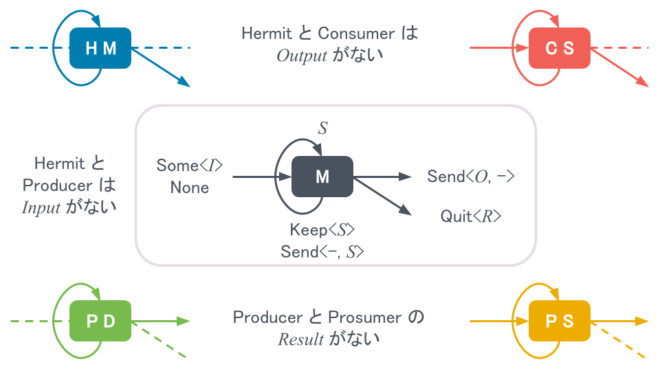
図式の詳細は記事全体を通して理解していただくとして、概要だけ先に書いておきます。

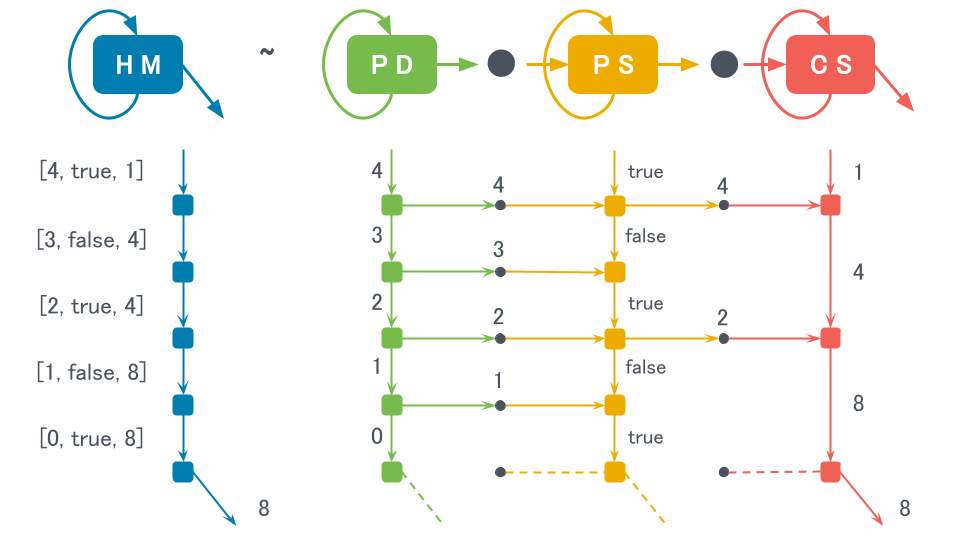
まず、図中の各アルファベットは略称です。 HMはHermit（隠遁者）の略です。同様に、PDはProducer（生産者）、CSはConsumer（消費者）、PSはProsumer（生産消費者）の略です。隠遁者、生産者、消費者、生産消費者の４つは状態機械の型またはインタフェースです。例えば、図式中のHMは隠遁者として振る舞う任意の状態機械を表しています。

次に、矢印ですが、状態機械から出て状態機械にくるりと戻ってくる矢印が状態を表しています。それ以外の真っ直ぐな矢印は、左から入ってくる矢印が入力です。右へ抜ける矢印が出力で、右下へ落ちる矢印が結果を意味します。出力と結果の違いは、出力が複数回（状態更新のたびに）値を送信する可能性があるのに対し、結果は一度しか値を返さない点です。入力も複数回（状態更新のたびに）値を受信する可能性があります。

黒丸（・）は状態機械の接続操作を表します。にょろにょろ（～）は同様に振る舞うことを意味します。

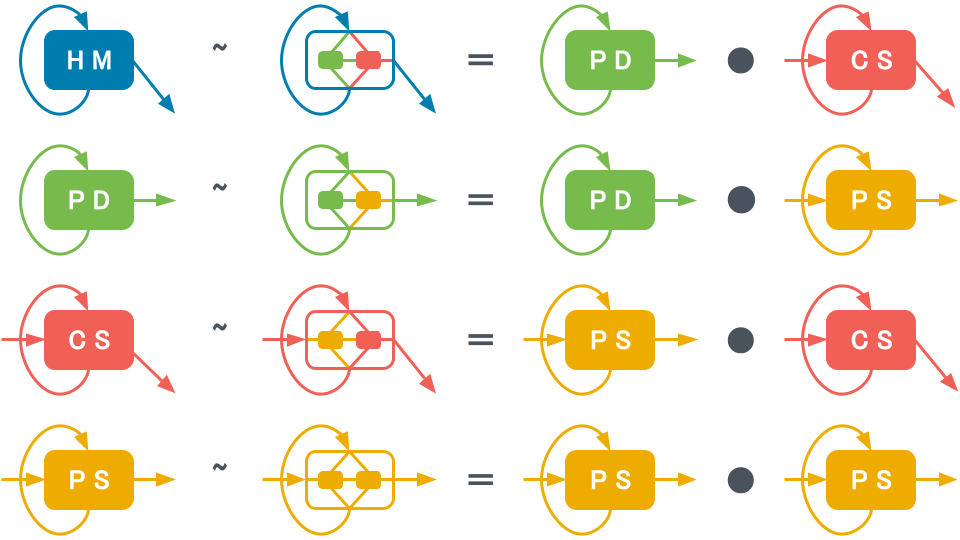
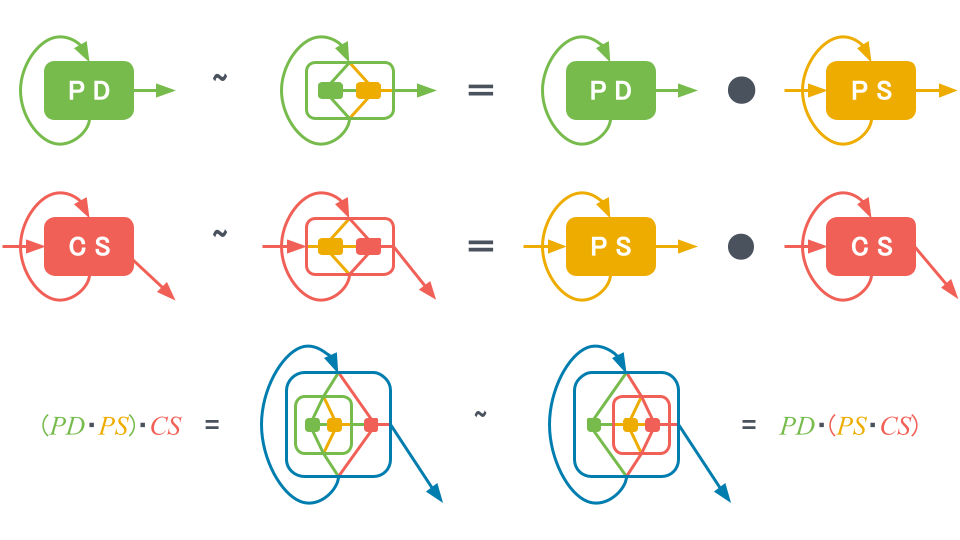
つまり、１つ目の式「HM～PD・CS」は「生産者（PD）と消費者（CS）の入出力を接続し、状態をひとまとめにすれば、隠遁者（HM）として振る舞う」と主張しています。他の３つの式「PD～PD・PS」、「CS～PS・CS」、「PS～PS・PS」も同様です。

ちなみに、隠遁者、生産者、消費者、生産消費者は一般的な用語ではありません。説明のために名付けた独自のもので、違和感があっても受け流していただけると助かります。また、状態機械や状態という概念は読み進めて行くうちに自然と掴めるはずです。

判別共用体

以降でよく使う関数と値のコードと、図での描き方を示します。なお、前節で述べた通り、使用言語はJavaScriptです。説明に必要なコードの断片は、つど貼り付けていきます。

// option
const some = value => ({ kind: "some", value });
const none = { kind: "none" };

// step
const send = (value, state) => ({ kind: "send", value, state });
const keep = state => ({ kind: "keep", state });
const quit = value => ({ kind: "quit", value });
const done = quit(undefined);

// option

const some = value => ({ kind: "some", value });

const none = { kind: "none" };

// step

const send = (value, state) => ({ kind: "send", value, state });

const keep = state => ({ kind: "keep", state });

const quit = value => ({ kind: "quit", value });

const done = quit(undefined);

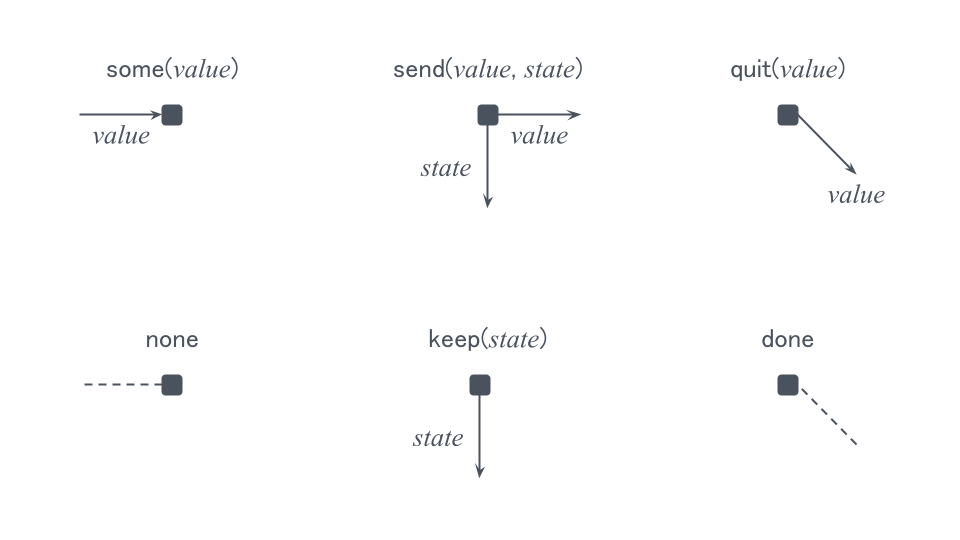
someやsend、keep、quitは、引数の値をプロパティへそのまま詰め込んだオブジェクトを作る関数です。例えば、send("値", "状態")の計算結果は{ kind: "send", value: "値", state: "状態" }になります。ほとんど略記のようなものです。以降、計算結果の形式では書かず、関数適用時の形式（send("値", "状態")など）で書くこととします。

これらの関数の戻り値のプロパティや、none、doneのプロパティの更新は想定していません。つまり、不変なオブジェクトとして扱います。また、コードの通り、共通してkindというプロパティを待っています。 kindプロパティを検査すれば、valueプロパティやstateプロパティを持っているか判別できます。つまり、判別共用体として扱います。

someの戻り値を図に描く際は接点に左から入ってくる矢印で表記します。状態機械への入力があることを表現しています。 noneを図に描く際は接点の左側に伸びる破線で表記します。状態機械への入力がないことを表現しています。

sendの戻り値を図に描く際は節点から右と下へ出ていく２つの矢印で表記します。右に出て行く矢印がvalueプロパティの値で、下に出て行く矢印がstateプロパティの値です。状態機械の出力と次の状態を表すために使います。

keepの戻り値を図に描く際は節点から下へ出ていく矢印で表記します。状態機械からの出力がなく、次の状態のみが返ってきたことを表現しています。

quitの戻り値を図に描く際は節点から右下へ出ていく矢印で表記します。状態機械が終了し、状態機械の結果が返ってきたことを表現しています。 doneもquitの戻り値ですが、特別に破線で表記します。状態機械が終了したことを表現しています。

状態機械

隠遁者、生産者、消費者、生産消費者の４つは状態機械の型であると述べました。これらは、ある型の派生型になります。その基底となるMachine型をTypeScript風に疑似的に書いたものを次に示します。また、どのような派生であるのか、イメージ図も示します。

// 疑似コード
type Machine<Input, State, Output, Result> = Readonly<{
    init: State,
    next: (state: State, option: Some<Input> | None) =>
        Send<Output, State> | Keep<State> | Quit<Result>
}>;

// 疑似コード

type Machine<Input, State, Output, Result> = Readonly<{

init: State,

next: (state: State, option: Some<Input> | None) =>

Send<Output, State> | Keep<State> | Quit<Result>

}>;

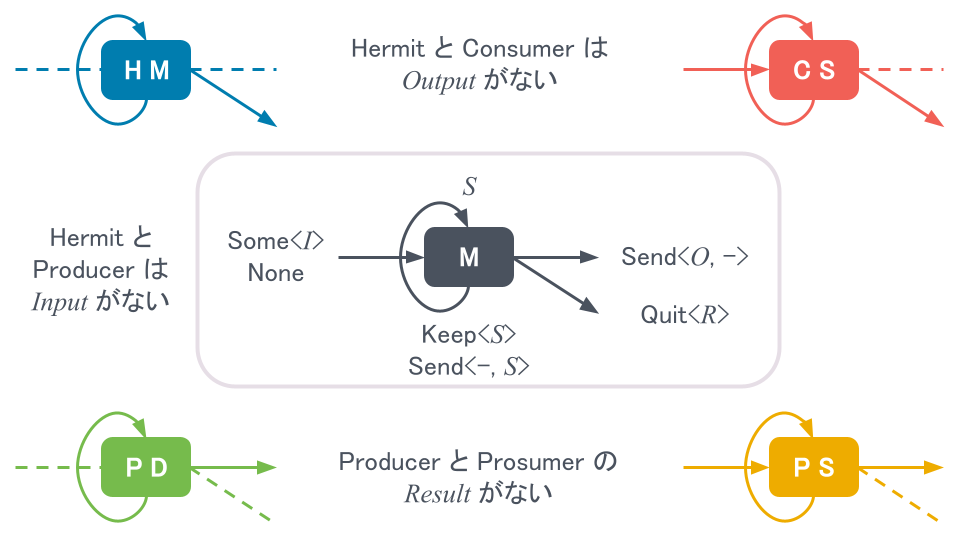
Machineの派生型である隠遁者は入力の型（Input）と出力の型（Output）をボトム型（値を持たない型）に制限した状態機械とみなせます。つまり、入出力のない、結果のみを返す状態機械を意味しています。ひたすらに状態を更新して、最後に結果を１つ返す状態機械です。

同様に、生産者は入力の型をボトム型、結果の型（Result）をユニット型（ただ１つの値を持つ型）に制限した状態機械とみなせます。入力と結果を返さない、出力のみを返す状態機械を意味しています。状態更新のたびに出力したり、しなかったりする状態機械です。

消費者は出力の型をボトム型に制限した状態機械とみなせます。入力と結果はありますが、出力のない状態機械を意味しています。現在状態と入力から状態を更新し、最後に結果を１つ返す状態機械です。

生産消費者は結果の型をユニット型に制限した状態機械とみなせます。つまり、入力と出力はありますが、結果は返さない状態機械を意味しています。現在状態と入力から状態を更新し、そのたびに出力したり、しなかったりする状態機械です。

隠遁者の具体例：階乗

隠遁者の具体例として階乗を取り上げます。自然数nの階乗はn!と表記し、自然数nから1までのすべての自然数の積で定義されます。例えば、4! = 4 × 3 × 2 × 1 = 24となります。

隠遁者として階乗を実装すると次のようなコードになります。また、run(factorial(4))の動作イメージ図も一緒に示しておきます。

function factorial(n) {
    return {
        init: [n, 1],
        next: ([i, acc]) => i > 0
            ? keep([i - 1, i * acc])
            : quit(acc)
    };
}

function run(hermit) {
    let step = keep(hermit.init);
    while(step.kind !== "quit") {
        step = hermit.next(step.state, none);
    }
    return step.value;
}

const resultHMa = run(factorial(4));
console.log(resultHMa); // =>  24

function factorial(n) {

return {

init: [n, 1],

next: ([i, acc]) => i > 0

? keep([i - 1, i * acc])

: quit(acc)

};

}

function run(hermit) {

let step = keep(hermit.init);

while(step.kind !== "quit") {

step = hermit.next(step.state, none);

}

return step.value;

}

const resultHMa = run(factorial(4));

console.log(resultHMa); // => 24

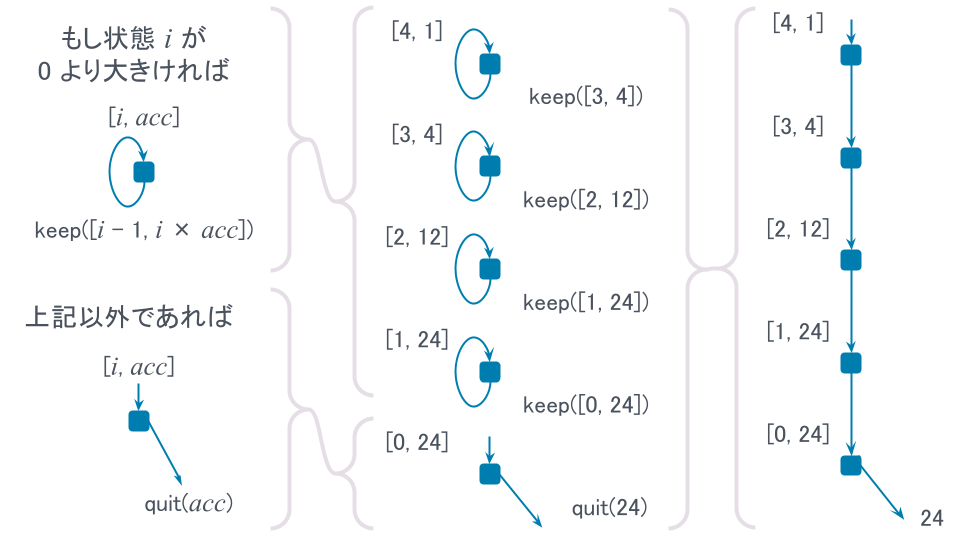
factorial(n)はn!を計算する隠遁者です。 runは隠遁者を動かし、結果を取り出す関数です。動作イメージの通り、run(factorial(4))は初期状態[4, 1]から順に状態を[3, 4]、[2, 12]…と更新していきます。そして最後に、結果として24が取り出されます。正しく階乗が計算できていますね。

注意点として、隠遁者単体では動作しません。 runで動かす必要があります。 runは次のように動作します。まず、隠遁者の初期状態（initプロパティ）から始めて、while文が回ります。 while文内で行うのは、隠遁者の状態遷移関数（nextメソッド）を使った状態更新です。状態遷移関数が結果を返してきた段階でwhile文を抜けて、結果を取り出して返します。

現在状態の保持と反復処理の責務はrunが担ってくれるため、その分、隠遁者の責務は小さくなります。すなわち、初期状態と、どのように状態を遷移させるかを決めることが、隠遁者の責務です。事実、factorialは初期状態と状態遷移のロジックしか実装されておらず、どのように反復すべきかは言及していません。

…実は、隠遁者の図には嘘があります。状態を表す矢印がくるりと隠遁者自身に戻ってきていますが、正確には途中で矢印が途切れているはずです。そして、途切れた矢印をrunが繋げることで、隠遁者は動きます。ただ、不正確であっても描きやすいので、このままくるりと繋げて描くことにします。

生産者の具体例：カウントダウン

生産者の具体例としてカウントダウンを取り上げます。カウントダウンは値をだんだん減らしていくものです。

生産者としてカウントダウンを実装すると次のようなコードになります。また、gun(countdown(4, 0)))の動作イメージ図も一緒に示しておきます。

function countdown(start, stop, step = 1) {
    return {
        init: start,
        next: i => i > stop
            ? send(i, i - step)
            : done
    };
}

function* gun(producer) {
    let step = keep(producer.init);
    while(step.kind !== "quit") {
        if(step.kind === "send") {
            yield step.value;
        }
        step = producer.next(step.state, none);
    }
}

for(const i of gun(countdown(4, 0)))
    console.log(i); // => 4 3 2 1

for(const i of gun(countdown(4, 0, 2)))
    console.log(i); // => 4 2

function countdown(start, stop, step = 1) {

return {

init: start,

next: i => i > stop

? send(i, i - step)

: done

};

}

function* gun(producer) {

let step = keep(producer.init);

while(step.kind !== "quit") {

if(step.kind === "send") {

yield step.value;

}

step = producer.next(step.state, none);

}

for(const i of gun(countdown(4, 0)))

console.log(i); // => 4 3 2 1

for(const i of gun(countdown(4, 0, 2)))

console.log(i); // => 4 2

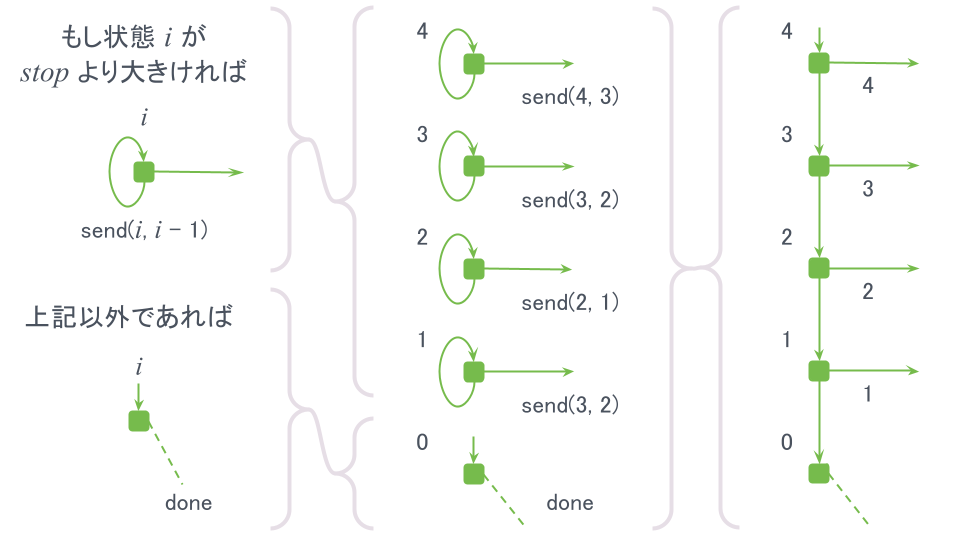
countdown(start, stop, step)はstartからstepづつ減算した値を出力する生産者です。 gunは生産者を動かし、出力を取り出すジェネレータ関数です。

動作イメージの通り、gun(countdown(4, 0)))は初期状態4から順に状態を3, 2…と更新していきます。その間に4, 3, 2, 1と出力し、最後に停止します。同様に、countdown(4, 0, 2)は4から2づつ値を減らしていくので、ひとつ飛ばしに4, 2と出力されます。

隠遁者と同様の注意点として、生産者単体では動作しません。 gunで動かす必要があります。 gunは次のように動作します。まず、生産者の初期状態から始めて、while文が回ります。 while文内で行うのは、隠遁者の状態遷移関数による状態更新と出力の取り出しです。次の状態が得られなければ、while文を抜けて終了します。

消費者の具体例：総乗

消費者の具体例として総乗を取り上げます。総乗は与えられた値をすべて乗算した値を求めるものです。総和の足し算を掛け算に変えたものと言えます。例えば、{5, 9, 2}の総乗は5×9×2=90となります。

ただ、複数の入力が必要となる消費者を動かすのは面倒です。そこで、総乗に値を渡すものとしてカウントダウンを使います。カウントダウンと総乗を接続することで、入力の面倒がなくなります。これは、生産者と消費者を接続すれば隠遁者として振る舞うという、「HM～PD・CS」の実例でもあります。

消費者として総乗を実装すると次のようなコードになります。また、productとrun(link(countdown(4, 0), product))の動作イメージ図も一緒に示しておきます。

なお、接続に使用しているlink関数の実装はこの節では示しません。「付録：状態機械の接続」の節で付録として示します。

const product = {
    init: 1,
    next: (acc, opt) => opt.kind === "some"
        ? keep(opt.value * acc)
        : quit(acc)
};

const resultCSa = run(link(countdown(4, 0), product));
console.log(resultCSa); // => 24

const resultCSb = run(link(countdown(4, 0, 2), product));
console.log(resultCSb); // => 8

const product = {

init: 1,

next: (acc, opt) => opt.kind === "some"

? keep(opt.value * acc)

: quit(acc)

};

const resultCSa = run(link(countdown(4, 0), product));

console.log(resultCSa); // => 24

const resultCSb = run(link(countdown(4, 0, 2), product));

console.log(resultCSb); // => 8

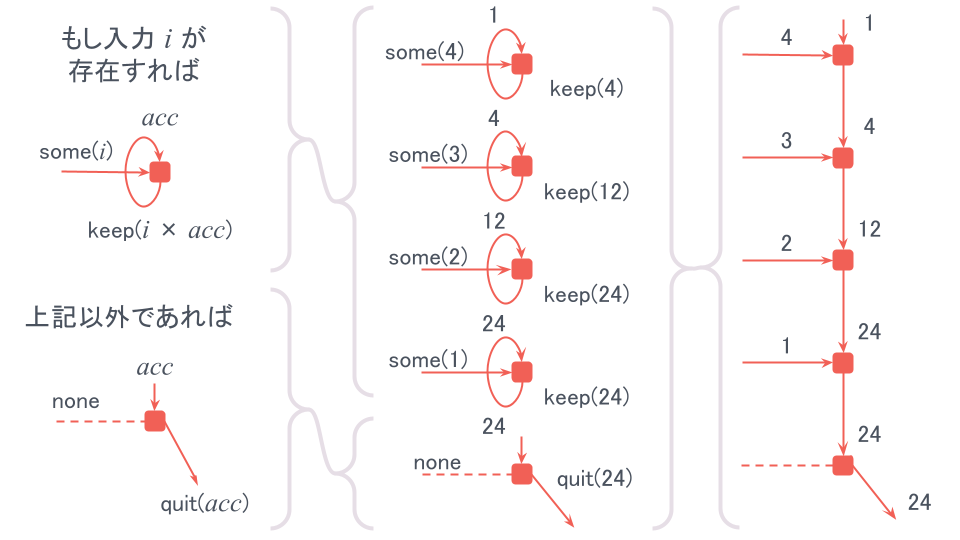
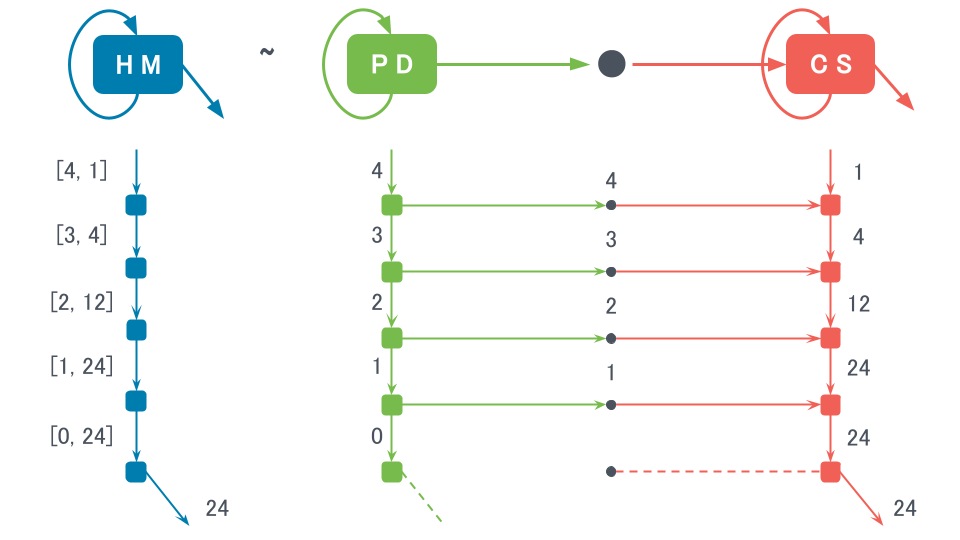
productは入力の値を乗算した値を状態として保持し、入力がなくなった段階で状態を結果として返しています。動作イメージの通り、run(link(countdown(4, 0), product))はcountdown(4, 0)が出力する4, 3, 2, 1をproductが乗算して保持しています。 productの状態は4, 12, 24, 24と更新され、最後に結果24を返しています。これは階乗の計算の定義と同じ計算をしています。つまり、カウントダウン（生産者）と総乗（消費者）を接続すると階乗（隠遁者）になるということです。

そして、隠遁者や生産者と同様に消費者も反復の責務は持っていません。また、生産者と消費者は接続の責務も持っていません。接続はlinkが一手に担っています。

ところで、数学には階乗によく似たものとして、二重階乗があります。自然数nの二重階乗はn!!と表記し、自然数nから1までのnと同じ偶奇性を持つ数だけをすべて掛けた積で定義されます。例えば、4!! = 4 × 2 = 8となります（4は偶数です）。

countdown(4, 0, 2)は4から2づつ値を減らしていくので、ひとつ飛ばしに4, 2と出力されます。これとproductを組み合わせれば二重階乗が計算できそうですね。実際、run(link(countdown(4, 0, 2), product))の計算結果は8になっています。

組み合わせを少し変えるだけで、階乗と二重階乗の計算が両方できてしまいました。素晴らしいですね。よく見ると順列の総数も計算できそうですが、生産者の例示はここで止めて次へ進みます。

生産消費者の具体例：ひとつ飛ばし

カウントダウンは偶然にもひとつ飛ばしの機能を持っていました。しかし、すべての生産者がひとつ飛ばしの機能を持っているとは限りません。そこで、ひとつ飛ばしの機能を生産消費者の具体例として切り出してみます。

ただ、複数の入力が必要となる生産消費者を動かすのは面倒です。そこで、生産者や消費者と組み合わせます。これは「PD～PD・PS」、「CS～PS・CS」の実例でもあります。

生産消費者としてひとつ飛ばしを実装すると次のようなコードになります。また、stepBy2とrun(link(link(countdown(4, 0), stepBy2), product))の動作イメージ図も一緒に示しておきます。

const stepBy2 = {
    init: true,
    next: (pass, opt) => opt.kind === "none"
        ? done
        : pass
            ? send(opt.value, false)
            : keep(true)
};

const pd_ps = link(countdown(4, 0), stepBy2);
for(const i of gun(pd_ps))
    console.log(i); //=> 4 2

const resultPSa = run(link(pd_ps, product));
console.log(resultPSa); // => 8

const ps_cs = link(stepBy2, product);
const resultPSb = run(link(countdown(4, 0), ps_cs));
console.log(resultPSb); // => 8

const stepBy2 = {

init: true,

next: (pass, opt) => opt.kind === "none"

? done

: pass

? send(opt.value, false)

: keep(true)

};

const pd_ps = link(countdown(4, 0), stepBy2);

for(const i of gun(pd_ps))

console.log(i); //=> 4 2

const resultPSa = run(link(pd_ps, product));

console.log(resultPSa); // => 8

const ps_cs = link(stepBy2, product);

const resultPSb = run(link(countdown(4, 0), ps_cs));

console.log(resultPSb); // => 8

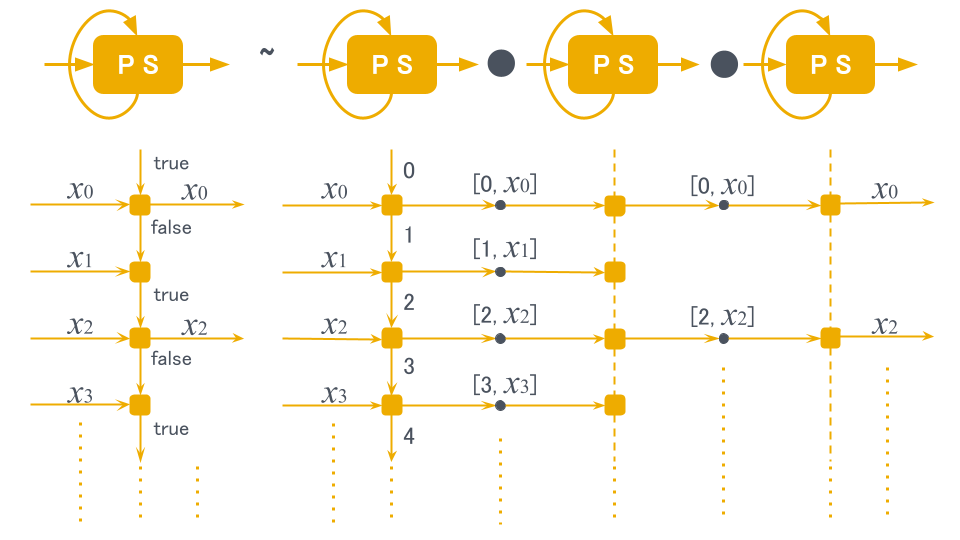
動作イメージの通り、stepBy2はひとつ飛ばしに入力の値を出力しています。

link(countdown(4, 0), stepBy2)が4, 2を出力することから、countdown(4, 0, 2)と同じ動作をすることがわかります。つまり、カウントダウン（生産者）とひとつ飛ばし（生産消費者）を接続すると、ひとつ飛ばしのカウントダウン（生産者）になるということです。

また、link(stepBy2, product)のようにひとつ飛ばし（生産消費者）と総乗（消費者）を先に接続し、生産者（カウントダウン）を最後に接続しても二重階乗（隠遁者）を正しく計算できています。生産者と接続して隠遁者になるのは消費者ですから、生産消費者と消費者を接続すると消費者として振る舞うことがわかります。

そして、隠遁者や生産者、消費者と同様に生産消費者も反復の責務は持っていません。また、生産者や消費者と同様に生産消費者も接続の責務は持っていません。

ところで、生産者と消費者のどちらと先に生産消費者を接続したかによらず、どちらも計算結果が8となっています。順序によって計算結果が変わらないことから、linkは結合性を持っている可能性があります。しかし、この記事の目標に厳密性は入っていないので、linkが結合律を満たすことは確認しません。ただ、linkの適用順序を図に書き込むと煩雑になってしまうので、この記事では結合律が成り立つと仮定して適用順序を省略して図示します。

生産消費者の再構築の具体例：ひとつ飛ばし

ここまでで、目標としていた4つの図式のうち上3つの式の例示ができました。残るは最後の式のみです。

やや強引な例ではありますが、ひとつ飛ばしの生産消費者を3つの生産消費者で再構築してみます。すなわち、入力にインデックスを付与して出力するwithIndex。入力が条件を満たす場合のみ出力するfilter。入力を変換して出力するmapの3つの生産消費者でstepBy2を再構築します。

具体的には次のようなコードになります。また、stepBy2_rebuildの動作イメージ図も一緒に示しておきます。

const withIndex = {
    init: 0,
    next: (i, option) => option.kind === "none"
        ? done
        : send([i, option.value], i + 1)
};

function filter(predicate) {
    return {
        init: undefined,
        next: (_, option) => option.kind === "none"
            ? done
            : predicate(option.value)
                ? send(option.value, _)
                : keep(_)
    };
};

function map(transformer) {
    return {
        init: undefined,
        next: (_, option) => option.kind === "none"
            ? done
            : send(transformer(option.value), _)
    };
};

const evenFst = filter(([i, _]) => i % 2 === 0);
const snd = map(([_, x]) => x);
const stepBy2_rebuild = link(withIndex, link(evenFst, snd));

const pd_ps_rebuild = link(countdown(4, 0), stepBy2_rebuild);
for(const i of gun(pd_ps_rebuild))
    console.log(i); //=> 4 2

const resultPSc = run(link(pd_ps_rebuild, product));
console.log(resultPSc); // => 8

const withIndex = {

init: 0,

next: (i, option) => option.kind === "none"

? done

: send([i, option.value], i + 1)

};

function filter(predicate) {

return {

init: undefined,

next: (_, option) => option.kind === "none"

? done

: predicate(option.value)

? send(option.value, _)

: keep(_)

};

function map(transformer) {

return {

init: undefined,

next: (_, option) => option.kind === "none"

? done

: send(transformer(option.value), _)

};

const evenFst = filter(([i, _]) => i % 2 === 0);

const snd = map(([_, x]) => x);

const stepBy2_rebuild = link(withIndex, link(evenFst, snd));

const pd_ps_rebuild = link(countdown(4, 0), stepBy2_rebuild);

for(const i of gun(pd_ps_rebuild))

console.log(i); //=> 4 2

const resultPSc = run(link(pd_ps_rebuild, product));

console.log(resultPSc); // => 8

コードが長いですね…。結論を先に述べれば、stepBy2_rebuildは、stepBy2を使った時と同じ出力と結果を返しています。つまり、生産消費者と生産消費者を接続すれば、生産消費者として振る舞うという、「PS～PS・PS」の実例になっています。

withIndexはインデックスとして状態を0から順に数え上げています。そして、インデックスと入力を２つ組（タプル）にして出力します。

filterは引数で与えられた述語関数に合格した入力を、そのまま出力します。したがって、filter(([i, _]) => i % 2 === 0)は入力のタプルの第一要素（インデックス）が偶数の場合のみ、そのまま出力する生産消費者となります。

mapは引数で与えられた関数を入力に適用して出力します。したがって、map(([_, x]) => x)は入力のタプルの第二要素（もともとの入力）を出力する生産消費者となります。

filterとmapはやや特殊な生産消費者で、状態はundefinedの１つの値しか取りません。もはや”状態”機械と言えるのか怪しいですね。ともかく、これら３つの生産消費者を組み合わせると、ひとつ飛ばしの生産消費者となります。

終わりに

いかがだったでしょうか。階乗や二重階乗という反復処理の具体例を通して、謎めいていた４つの図式「HM～PD・CS」、「PD～PD・PS」、「CS～PS・CS」、「PS～PS・PS」を説明してみました。反復の分解と再構築ができることに実感を持っていただけたら幸いです。最後まで読んでいただき、ありがとうございました。

付録：状態機械の接続

付録です。

linkの実装は次の通りになります。また、状態遷移関数の中身を説明するための図も一緒に示しておきます。

function link(left, right) {
    return {
        init: [some(left.init), right.init],
        next: ([stateL, stateR], option) => {
            const stepL = stateL.kind === "none"
                ? done
                : left.next(stateL.value, option);

            const optionL = stepL.kind === "send"
                ? some(stepL.value)
                : none;

            const stepR = stepL.kind === "keep"
                ? keep(stateR)
                : right.next(stateR, optionL);

            if(stepR.kind === "quit")
                return stepR;

            const state = stepL.kind === "quit"
                ? [none, stepR.state]
                : [some(stepL.state), stepR.state];

            return stepR.kind === "keep"
                ? keep(state)
                : send(stepR.value, state);
        }
    };
}

function link(left, right) {

return {

init: [some(left.init), right.init],

next: ([stateL, stateR], option) => {

const stepL = stateL.kind === "none"

? done

: left.next(stateL.value, option);

const optionL = stepL.kind === "send"

? some(stepL.value)

: none;

const stepR = stepL.kind === "keep"

? keep(stateR)

: right.next(stateR, optionL);

if(stepR.kind === "quit")

return stepR;

const state = stepL.kind === "quit"

? [none, stepR.state]

: [some(stepL.state), stepR.state];

return stepR.kind === "keep"

? keep(state)

: send(stepR.value, state);

}

};

}

linkは２つの状態機械left（左）とright（右）を引数に取り、それら接続した新たな状態機械を返します。新たな状態機械の初期状態は、左右の初期状態の組です。

ただし、左の初期状態のみsomeが適用されています。これは、左が終了した後も、右が継続して動く可能性があるためです。例えば、入力を逆順に出力するreverseは、reverseから見て左側の状態機械が停止しても継続稼働します。なぜなら、reverseは入力値をすべて累積し、左が停止した後に、累積した入力を逆順に出力するからです。

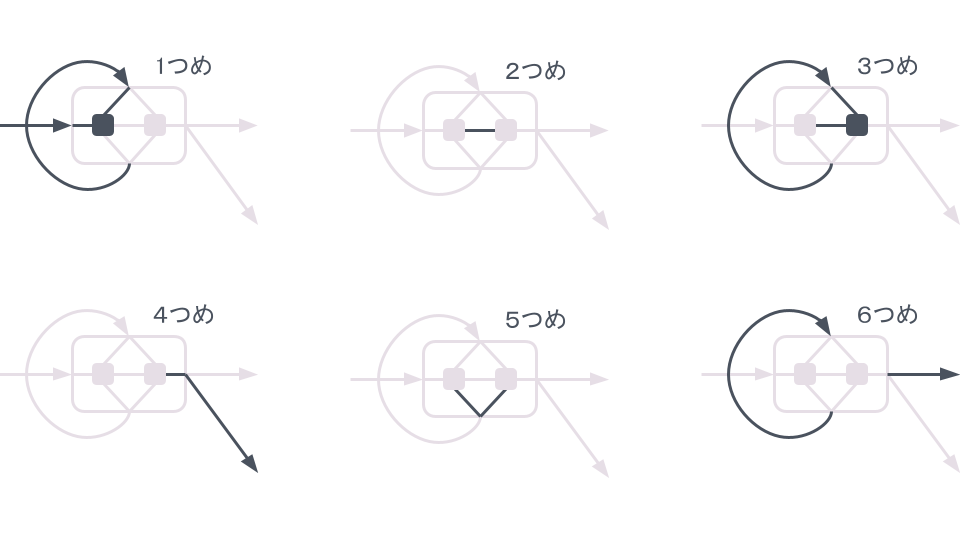
さて、見るからに複雑なのが状態遷移関数です。６つの条件分岐から構成されています。コードと一緒につけた６つの図は、６つの条件分岐とそれぞれ対応しています。

１つ目の条件分岐は、左の状態が存在するかどうかを調べています。左の状態が存在しない場合、すでに左は停止しています。そこで、左の状態遷移関数がdoneを返したとみなします。また、左の状態が存在する場合は、左の状態遷移関数で状態を遷移させます。その際に、全体の入力optionをそのまま、左の状態遷移関数に渡します。

２つ目の条件分岐は、１つ目の条件分岐の計算によって左の出力が得られたかを調べています。出力が得られた場合は、出力にsomeを適用します。出力が得られない場合は、noneとします。これによって、右の状態遷移関数の入力を作成します。

３つ目の条件分岐は、１つ目の条件分岐の計算によって左が出力せず、停止もしていないことを調べています。左の出力がなく、停止もしていない場合は、右の状態遷移は飛ばし、右の状態をそのまま保持します。左の出力がある、もしくは左が停止している場合は、右の状態遷移関数で状態を遷移させます。その際に、２つ目の条件分岐の計算によって得られた入力を、右の状態遷移関数に渡します。

この右の状態遷移を飛ばす機能により、filterなどが実現できています。

４つ目の条件分岐は、３つ目の条件分岐の計算により右が停止したか、または結果を返したか調べています。右が停止、もしくは結果を返した場合、全体としても停止するか結果を返します。したがって、左の状態機械の終了を待たずに右の状態機械は停止することがあり、全体としても停止する可能性があります。

これにより、有限の状態遷移で停止する生産消費者や消費者と接続することで、無限に出力する生産者を扱うことができます。また、入力を消費しつくすことなく停止できるため、ある種の消費者を効率よく実装できます。例えば、条件を満たす最初の要素を見つけるfindは、要素を見つけた時点で停止できます。

５つ目の条件分岐は、１つ目の条件分岐の計算によって左の状態が得られたかを調べています。先に述べた通り、左が停止しても右は継続する可能性があります。そのため、左の状態があればsomeを適用しておき、なければnoneで代替します。

６つ目の条件分岐は、３つ目の条件分岐の計算により右の出力が得られたかを調べています。出力が得られれば、全体としても出力と状態を返し、そうでなければ状態のみを返します。

以上がlinkの動作になります。複雑な動作ですね。このような複雑さは、４つの図式の理解には不要だろうと思い、付録にしました。

あ、この付録まで読みこなした方は一声かけてください。全力で頼りにさせていただきます（ニッコリ）。

shunki

目次

この記事の目標

判別共用体

状態機械

隠遁者の具体例：階乗

生産者の具体例：カウントダウン

消費者の具体例：総乗

生産消費者の具体例：ひとつ飛ばし

生産消費者の再構築の具体例：ひとつ飛ばし

終わりに

付録：状態機械の接続

おすすめ

input, textarea中のキャレット座標 (カーソルの位置) を取得する

低コストでAI同士で会話し続けるページを作ってみた

ブラウザでもmocopiしたい