はじめに
おはようございます。こんにちは。こんばんは。GMOアドマーケティングのY-Kです。
今回は機械学習への足がかりとなるような記事を書きたいと思ったので、クラスタリングタスクを通して機械学習の流れを大雑把に書いていこうと思います。
機械学習における基本的な データ分析 -> 予測 -> 評価の流れを体験しつつ、読んでいる間に気になるところがあればそこを深掘りしていくなど、機械学習への興味/勉強の第一歩としていただければと思います。
クラスタリングとは
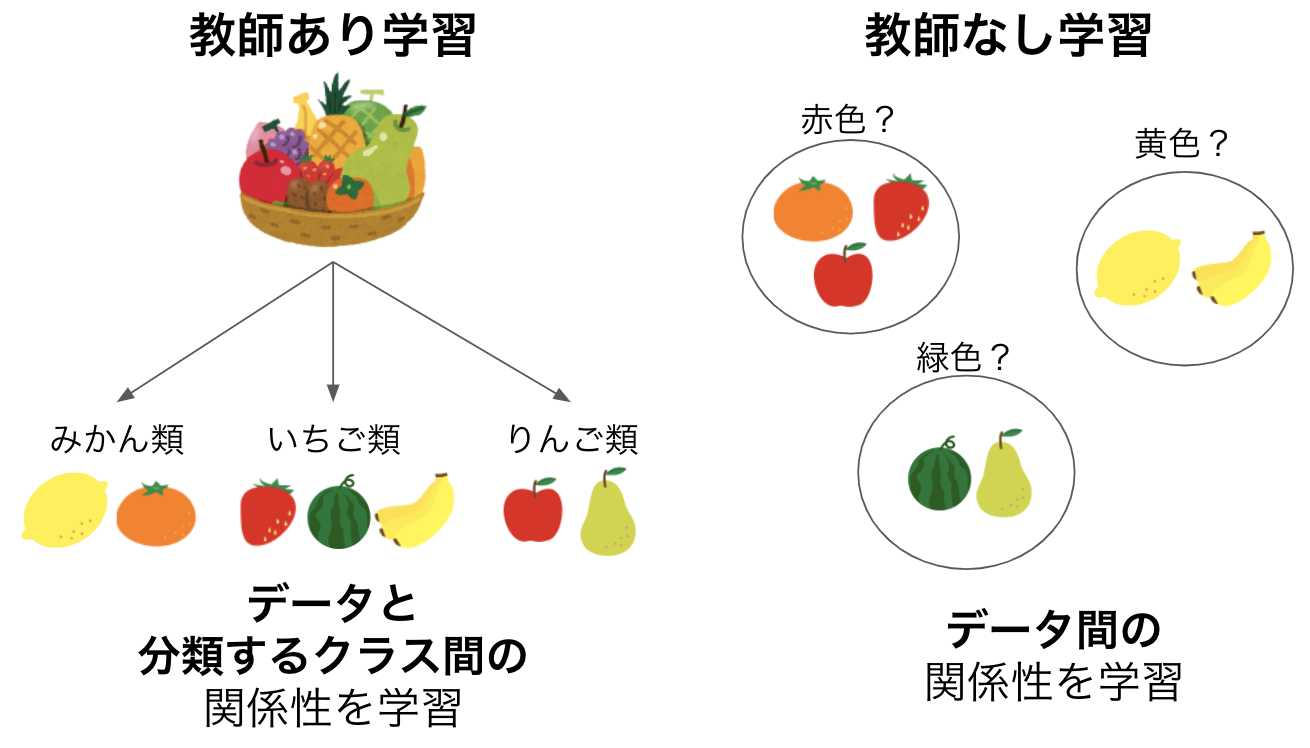
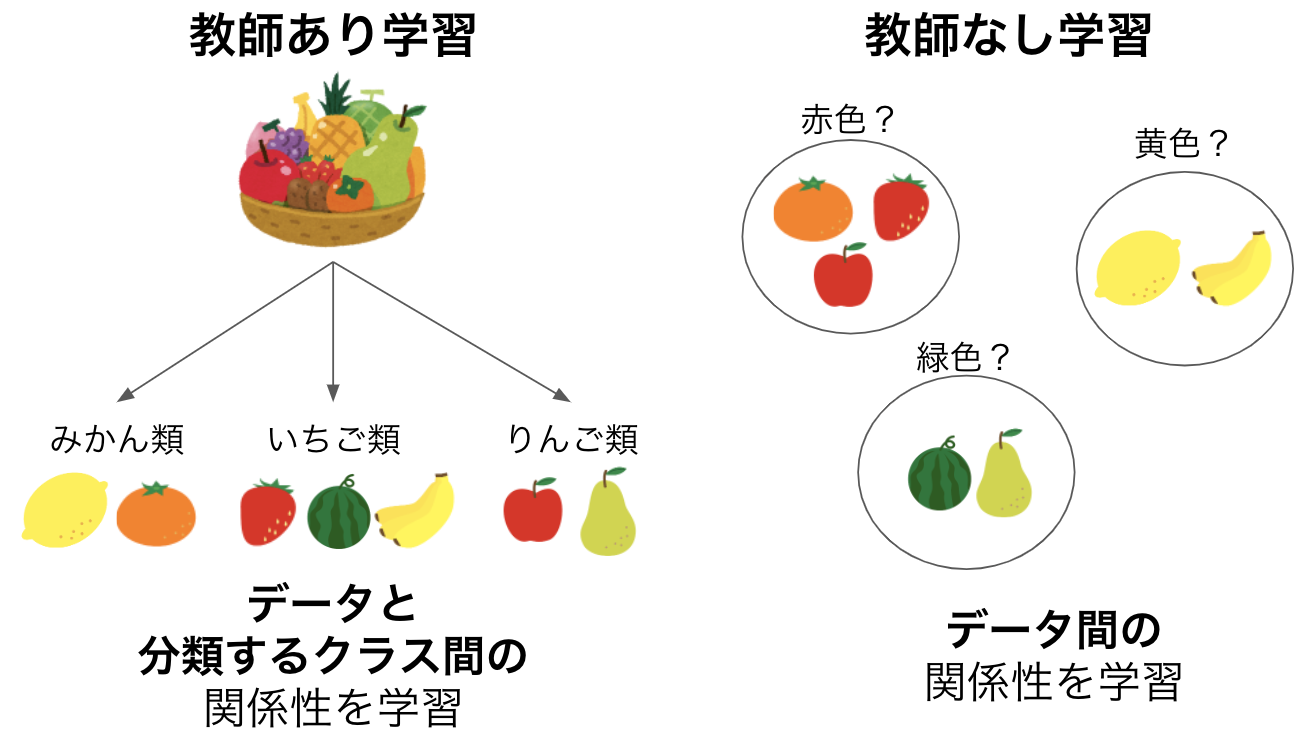
クラスタリングは機械学習における教師なし学習の一種で、データの類似度でデータをグループ(クラスタ)分けする手法のことを指します。データに対して答えが存在する教師あり学習とは異なり、各データに答えがない状態で学習されるので、クラスタリングによってまとめられたデータのグループが何を示しているのかは解釈が必要となります。
しかしその分、クラスタリングは教師あり学習の分類と比べてデータ同士の繋がりに重きをおいて学習することができます。
今回行うタスク
クラスタ数が不明なデータにおいてクラスタリングを行い、結果を評価していくことで、分類に最適なクラスタ数を考えようと思います。環境
google colaboratory上で、機械学習向けライブラリscikit-learnを用いて行います。データ作成
まずはscikit-learnのmake_blobs関数で分析対象のデータを生成します。サンプル数やクラスタの数、特徴量の数を指定することでクラス分類タスク用のデータを生成することができます。
詳しい使い方はドキュメントを参考にしてください。
クラスタの数は3~10個の間でランダム、特徴量は大人の事情で2つに設定します。
|
1 2 3 4 5 6 7 8 9 |
from sklearn.datasets import make_blobs import random centers = random.randint(3, 10) data, cluster_labels = make_blobs(n_samples=500, #サンプル数 centers=centers, #クラスタの数 n_features=2, #特徴量の数 cluster_std=1 #クラスタ内の分布のばらつき具合 ) |
分析
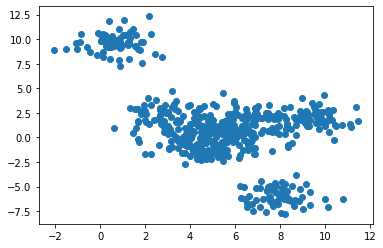
百聞は一見にしかずということで、生成したデータを可視化して確認します。大人の事情で特徴量を2つにしたので、2次元のグラフにプロットすることができます。
|
1 2 3 |
import matplotlib.pyplot as plt plt.scatter(data[:, 0], data[:, 1]) |
|
1 2 3 4 5 6 7 8 |
from sklearn import preprocessing # 標準化 sc = preprocessing.StandardScaler() data_norm = sc.fit_transform(data) # 標準化した後のデータ分布を確認 plt.scatter(data_norm[:, 0], data_norm[:, 1]) |

特徴量がグラフで表現できない4つ以上の場合は、主成分分析や深層学習でデータを変換することで次元削減し、グラフ描写が可能な次元数まで特徴量を落として分析を行います。
データ量や特徴量が多くなればなるほど分析にかかる時間が膨大になっていきます。
(4次元以上のデータに対して次元削減を行いクラスタリングするタスクについては今度執筆しようと思います。)
予測
クラスタリングの方法は数多くあるのですが、今回はk-means法で行います。例の如くscikit-learnでモデルが準備されているのでそれを用います。
分類するクラスタ数を設定してデータを渡して学習を行います。
学習後、データの分類推測結果とクラスタの中心をプロットして確認してみます。
|
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn.cluster import KMeans #モデル作成 km = KMeans(n_clusters=3, random_state=0) #学習 km.fit(data_norm) #結果を可視化 plt.scatter(data_norm[:, 0], data_norm[:, 1], c=km.labels_) plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], color='red', marker='*', s=200) |
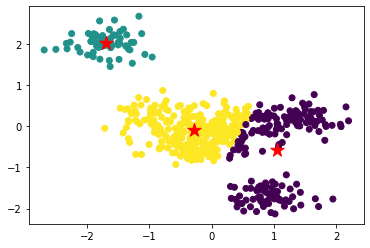
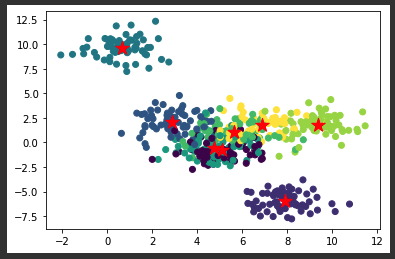
アルゴリズム的には図のように分類されました。
なんだか腑に落ちませんね。
ということで、クラスタ数を2~10で指定して力ずくでモデルを作成し、それぞれでクラスタリングしてみます。
lossは後々使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
model_list = [KMeans(n_clusters=i, random_state=0) for i in range(2, 11)] pred_list = [] center_list = [] loss_list = [] for i in range(len(model_list)): model_list[i].fit(data_norm) pred_list.append(model_list[i].labels_) center_list.append(model_list[i].cluster_centers_) loss_list.append(model_list[i].inertia_) plt.figure(figsize=(9, 9)) for i in range(len(pred_list)): plt.subplot(3, 3, i+1) plt.scatter(data_norm[:, 0], data_norm[:, 1], c=pred_list[i]) plt.scatter(center_list[i][:, 0], center_list[i][:, 1], color='red', marker='*', s=200) plt.show() |

4個以上はどれでもうまく分割できているように感じます。
評価
それでは、ここからはいくつのクラスタに分割すれば良いかを数値的に評価していきます。先程のモデルでどれが一番うまく分割できているかを結論付けます。 評価は以下の手法で行います。
- エルボー法
- シルエット分析
エルボー法
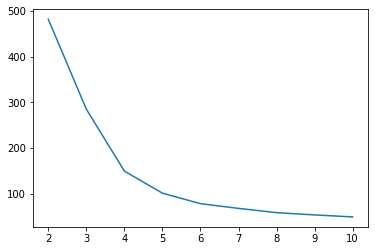
エルボー法は、各クラスター内の二乗誤差の総和を用いて最適なクラスタ数を導き出す手法です。クラスタ数ごとに誤差をプロットし、誤差が急激に減少している部分において誤差が最も小さい点を最適なクラスター数と推測します。
(グラフを腕に見立てた時の肘の部分です)
k-meansでは学習後、.inertia_から取得できます。
先ほどモデルをまとめて作成するときにloss_listに各モデルの誤差を格納していたので、それをプロットしてみます。
|
1 2 3 |
plt.plot(range(2,11), loss_list) plt.xticks(range(2,11)) plt.show() |
シルエット分析
シルエット分析とは以下の観点からモデルのクラスタリング性能を評価する方法です。- クラスタ内のサンプルは密であればあるほど=サイズが小さいほど良い(凝集度:α)
- 異なるクラスタは距離が離れていれば離れているほど良い(乖離度:β)
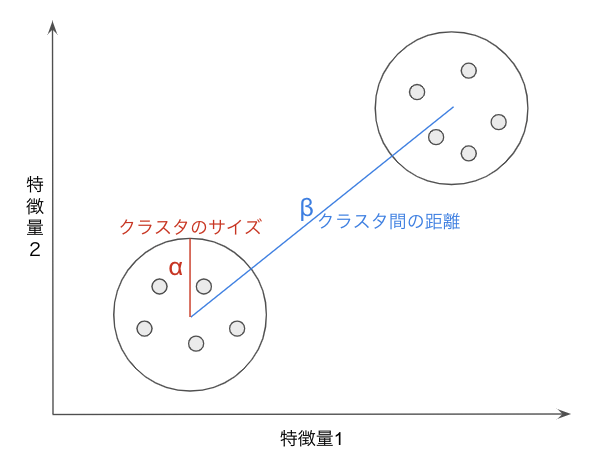
|
1 2 3 |
凝縮度:α = 各サンプルにおいて、同じクラスタに所属する他サンプルとの平均距離 乖離度:β = 各サンプルにおいて、最も近い別クラスタに所属するサンプルとの平均距離 シルエット係数 = (β - α) / MAX(α, β) |
- 正:そのサンプルが所属外のクラスタから離れている
- 0 :クラスタの境界付近に存在している
- 負:誤ったクラスタに所属している可能性が存在する
- サンプルの所属クラスタの番号でソート
- 同じクラスタ内ではシルエット係数でソート
クラスタリングに使用したデータと学習したクラスタリングモデルを渡し、シルエット図、クラスタごとのサンプル数、シルエット係数の平均値を表示する関数を作成します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
def silhouette_evaluate(data, km): cluster_labels=np.unique(km.labels_) silhouette_vals=silhouette_samples(data, km.labels_) y_ax_upper = 0 y_ax_lower = 0 yticks=[] print(f"クラスタ数:{len(cluster_labels)}") for i, class_label in enumerate(cluster_labels): c_silhouette_vals = silhouette_vals[km.labels_==class_label] print(f"{i}: {len(c_silhouette_vals)}") c_silhouette_vals.sort() y_ax_upper += len(c_silhouette_vals) plt.barh(range(y_ax_lower,y_ax_upper), c_silhouette_vals, height=1.0, edgecolor="none", ) yticks.append((y_ax_lower+y_ax_upper)/2.) y_ax_lower += len(c_silhouette_vals) silhouette_avg=np.mean(silhouette_vals) plt.axvline(silhouette_avg,color="red",linestyle="--") plt.ylabel("Cluster") plt.xlabel("Silhouette Coefficient") plt.yticks(yticks,cluster_labels + 1) plt.show() print(f"シルエット係数:{silhouette_avg}") print() |
|
1 |
silhouette_evaluate(data_norm, model_list[3]) |
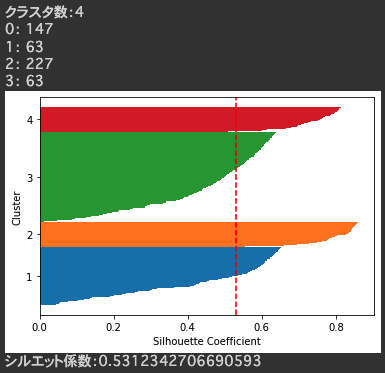
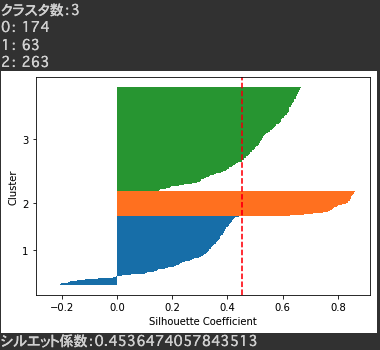
シルエット図は以下に注目します。
- シルエット係数が正のサンプルが多いこと
- 各クラスタの厚さが均等であること
- 適切にクラスタリングができているとクラスタ数は均等になる
各モデルのシルエット図を確認していくと、クラスタ数8,9あたりで綺麗なシルエット図ができていました。
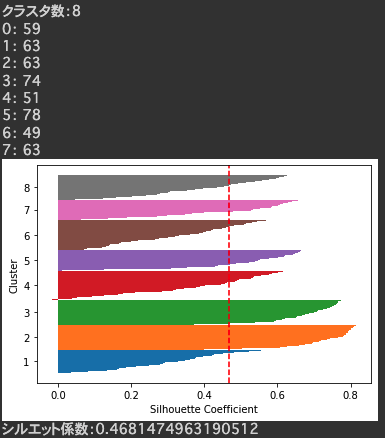
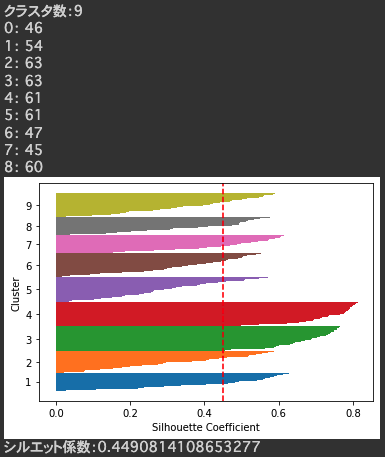
正解を確認してみると、こちらも8つのクラスタからできているデータでした。
(分布は大きく異なりますが・・・・)
最後に
今回は、クラスタ数が不明なデータに対して最適なクラスタ数の推定を行いました。機械学習への勉強の足がかりとなれば幸いです。
以上、ここまで読んでいただきありがとうございました。